题目内容
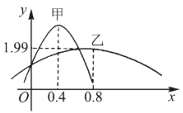
【题目】设l为曲线C:![]() 在点
在点![]() 处的切线.
处的切线.
(1)求l的方程;
(2)证明:除切点![]() 之外,曲线C在直线l的下方;
之外,曲线C在直线l的下方;
(3)求证:![]() (其中
(其中![]() ,
,![]() ).
).
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)求出切点处切线斜率,代入点斜式方程,可以求解;
(2)利用导数分析函数的单调性,进而分析出函数图象的形状,可得结论;
(3)法一,充分利用(2)的结果,对不等式左端进行放大,进一步放大为可以列项相消的形式来证明,法二,利用数学归纳法证明即可.
(1)设![]() (
(![]() ),则
),则![]() (
(![]() ),
),
从而曲线在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
于是切线方程为![]() ,即
,即![]() ,
,
因此直线l的方程为![]() .
.
(2)令![]() (
(![]() ),
),
则除切点![]() 之外,曲线C在直线l的下方等价于
之外,曲线C在直线l的下方等价于![]() (任意
(任意![]() ,
,![]() )恒成立.
)恒成立.
![]() 满足
满足![]() ,且
,且![]() (
(![]() ,
,![]() ),
),
当![]() 时,
时,![]() ,
,![]() ,从而
,从而![]() ,于是
,于是![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() ,从而
,从而![]() ,于是
,于是![]() 在
在![]() 单调递增.
单调递增.
因此![]() (任意
(任意![]() ,
,![]() ),除切点
),除切点![]() 之外,曲线C在直线l的下方.
之外,曲线C在直线l的下方.
(3)方法1 由(2)可知![]() (任意
(任意![]() ,
,![]() ).
).
令![]() 得
得![]() ,即
,即![]() .
.
则![]() ,
,![]() ,…,
,…,![]() .
.
将以上各式相加得![]()
![]() ,
,
当![]() ,
,![]() 时,
时,![]() ,
,
![]() ,
,
![]()
![]() ,
,
所以当![]() ,
,![]() 时,
时,![]() ,结论成立.
,结论成立.
方法2:用数学归纳法证明:
①当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,左边
,左边![]() 右边,不等式成立.
右边,不等式成立.
②假设当![]() (
(![]() ,
,![]() )时,不等式成立,
)时,不等式成立,
即![]() ,
,
当![]() 时,
时,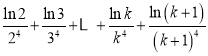
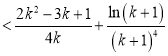 ,
,
只需证明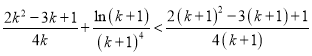 (*)
(*)
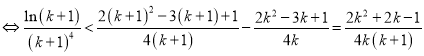
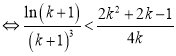 (**).
(**).
由(2)可知![]() (任意
(任意![]() ,
,![]() ),
),
则![]() (
(![]() ).
).
又当![]() ,
,![]() 时,
时,![]() ,
,
![]() ,
,
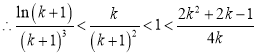 (
(![]() ).
).
所以(**)成立,从而(*)成立.
![]() 时,不等式成立.
时,不等式成立.
由①②可知,当![]() ,
,![]() 时,
时,![]() 成立.
成立.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案【题目】某水果经销商为了对一批刚上市水果进行合理定价,将该水果按事先拟定的价格进行试销,得到一组销售数据,如表所示:
试销单价 | 16 | 17 | 18 | 19 | 20 |
日销售量 | 168 | 146 | 120 | 90 | 56 |
(1)已知变量![]() 具有线性相关关系,求该水果日销售量
具有线性相关关系,求该水果日销售量![]() (公斤)关于试销单价
(公斤)关于试销单价![]() (元/公斤)的线性回归方程,并据此分析销售单价
(元/公斤)的线性回归方程,并据此分析销售单价![]() 时,日销售量的变化情况;
时,日销售量的变化情况;
(2)若该水果进价为每公斤![]() 元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价
元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价![]()
![]() 应定为多少元?
应定为多少元?
(参考数据及公式:![]() ,
,![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,
,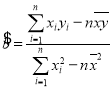 ,
,![]() )
)