题目内容
已知函数
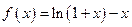 ,数列
,数列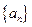 满足:
满足: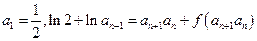 .
.(Ⅰ)求证:
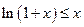 ;
;(Ⅱ)求数列
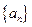 的通项公式;
的通项公式;(Ⅲ)求证不等式:
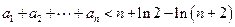
如下
(Ⅰ)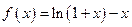
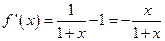
当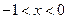 时,
时,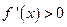 ,即
,即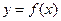 是单调递增函数;
是单调递增函数;
当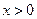 时,
时,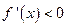 ,即
,即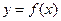 是单调递减函数;
是单调递减函数;
所以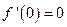 ,即
,即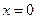 是极大值点,也是最大值点
是极大值点,也是最大值点
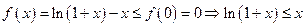 ,当
,当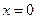 时取到等号. 5分
时取到等号. 5分
(Ⅱ)由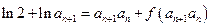 得
得
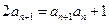
方法1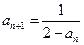
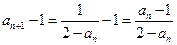
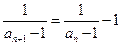
即数列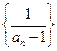 是等差数列,首项为
是等差数列,首项为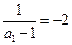 ,公差为
,公差为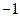
∴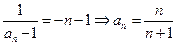
方法2利用函数不动点
方法3利用观察、归纳、猜想、数学归纳法证明
(Ⅲ)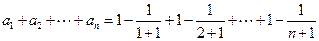
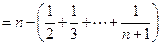
又∵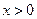 时,有
时,有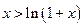
令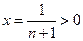 ,则
,则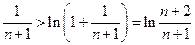
∴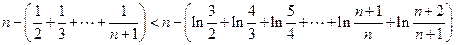
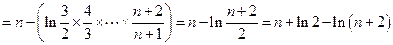
∴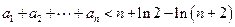
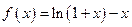
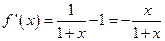
当
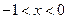 时,
时,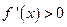 ,即
,即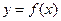 是单调递增函数;
是单调递增函数;当
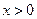 时,
时,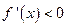 ,即
,即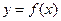 是单调递减函数;
是单调递减函数;所以
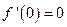 ,即
,即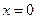 是极大值点,也是最大值点
是极大值点,也是最大值点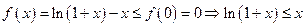 ,当
,当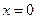 时取到等号. 5分
时取到等号. 5分(Ⅱ)由
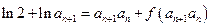 得
得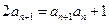
方法1
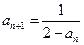
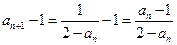
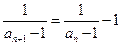
即数列
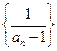 是等差数列,首项为
是等差数列,首项为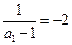 ,公差为
,公差为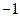
∴
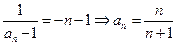
方法2利用函数不动点
方法3利用观察、归纳、猜想、数学归纳法证明
(Ⅲ)
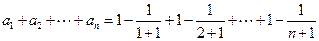
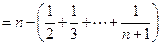
又∵
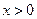 时,有
时,有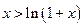
令
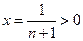 ,则
,则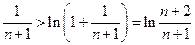
∴
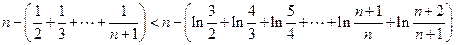
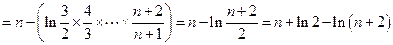
∴

练习册系列答案
相关题目
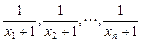 为等差数列.
为等差数列.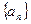 是等差数列,且
是等差数列,且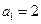 ,
,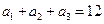 .
.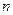 项和
项和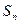 ;
;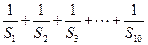 的值.
的值.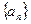 是递增数列,前n项和为
是递增数列,前n项和为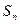 ,且
,且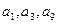 成等比数列,
成等比数列,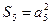 .求数列
.求数列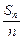 -1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.
-1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.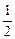 ,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.
,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.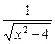 (x<-2).
(x<-2).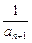 =-f--1(an)(n∈N*),求an;
=-f--1(an)(n∈N*),求an;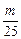 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.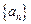 中,
中,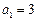 ,
,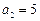 ,其前
,其前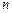 项和
项和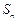 满足
满足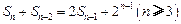 .令
.令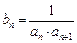 .
.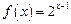 ,求证:
,求证: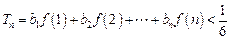 (
(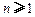 );
);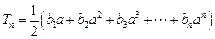 (
(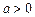 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有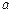 的值:①对于任意正整数
的值:①对于任意正整数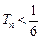 ;②对于任意的
;②对于任意的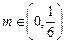 ,均存在
,均存在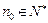 ,使得
,使得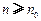 时,
时,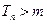 .
.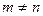 ,且
,且 和
和 都是等差数列,则
都是等差数列,则
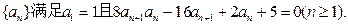 求数列
求数列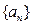 的通项公式.
的通项公式.