题目内容
(本小题满分14分)已知数列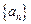 中,
中,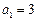 ,
,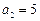 ,其前
,其前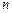 项和
项和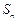 满足
满足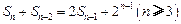 .令
.令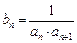 .
.
(Ⅰ)求数列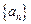 的通项公式;
的通项公式;
(Ⅱ)若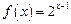 ,求证:
,求证: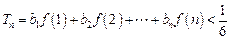 (
(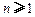 );
);
(Ⅲ)令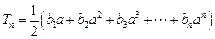 (
(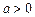 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有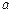 的值:①对于任意正整数
的值:①对于任意正整数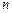 ,都有
,都有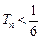 ;②对于任意的
;②对于任意的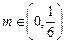 ,均存在
,均存在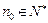 ,使得
,使得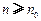 时,
时,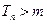 .
.
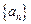 中,
中,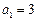 ,
,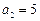 ,其前
,其前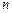 项和
项和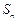 满足
满足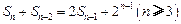 .令
.令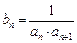 .
.(Ⅰ)求数列
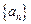 的通项公式;
的通项公式;(Ⅱ)若
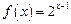 ,求证:
,求证: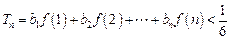 (
(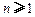 );
);(Ⅲ)令
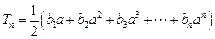 (
(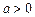 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有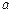 的值:①对于任意正整数
的值:①对于任意正整数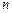 ,都有
,都有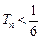 ;②对于任意的
;②对于任意的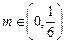 ,均存在
,均存在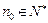 ,使得
,使得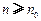 时,
时,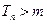 .
.(Ⅰ)由题意知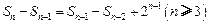 即
即 ……1′
……1′
∴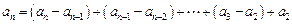
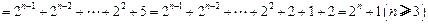 ……2′
……2′
检验知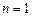 、
、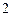 时,结论也成立,故
时,结论也成立,故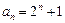 .…………3′
.…………3′
(Ⅱ)由于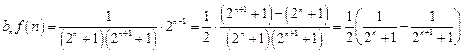
故
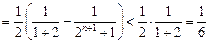 .…………6′
.…………6′
(Ⅲ)(ⅰ)当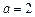 时,由(Ⅱ)知:
时,由(Ⅱ)知: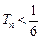 ,即条件①满足;又
,即条件①满足;又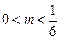 ,
,
∴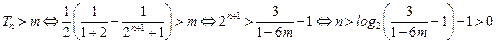 .
.
取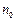 等于不超过
等于不超过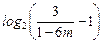 的最大整数,则当
的最大整数,则当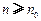 时,
时,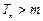 .…9′
.…9′
(ⅱ)当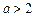 时,∵
时,∵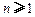 ,
,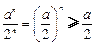 ,∴
,∴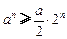 ,∴
,∴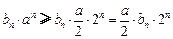 .
.
∴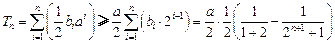 .
.
由(ⅰ)知存在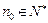 ,当
,当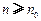 时,
时,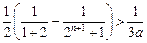 ,
,
故存在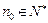 ,当
,当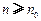 时,
时,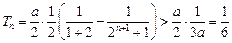 ,不满足条件. …12′
,不满足条件. …12′
(ⅲ)当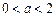 时,∵
时,∵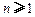 ,
,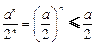 ,∴
,∴ ,∴
,∴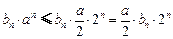 .
.
∴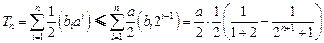 .
.
取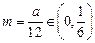 ,若存在
,若存在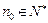 ,当
,当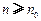 时,
时,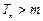 ,则
,则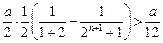 .
.
∴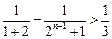 矛盾. 故不存在
矛盾. 故不存在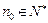 ,当
,当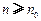 时,
时,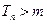 .不满足条件.
.不满足条件.
综上所述:只有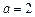 时满足条件,故
时满足条件,故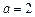 .…………14′
.…………14′
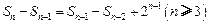 即
即 ……1′
……1′∴
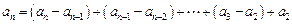
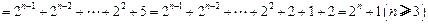 ……2′
……2′检验知
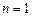 、
、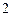 时,结论也成立,故
时,结论也成立,故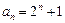 .…………3′
.…………3′(Ⅱ)由于
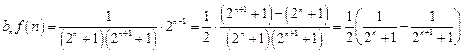
故

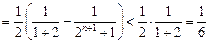 .…………6′
.…………6′(Ⅲ)(ⅰ)当
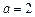 时,由(Ⅱ)知:
时,由(Ⅱ)知: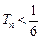 ,即条件①满足;又
,即条件①满足;又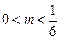 ,
,∴
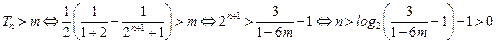 .
.取
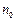 等于不超过
等于不超过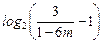 的最大整数,则当
的最大整数,则当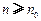 时,
时,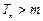 .…9′
.…9′(ⅱ)当
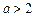 时,∵
时,∵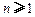 ,
,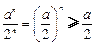 ,∴
,∴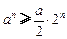 ,∴
,∴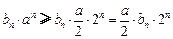 .
.∴
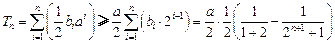 .
.由(ⅰ)知存在
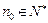 ,当
,当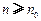 时,
时,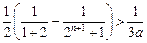 ,
,故存在
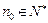 ,当
,当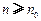 时,
时,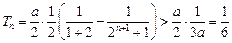 ,不满足条件. …12′
,不满足条件. …12′(ⅲ)当
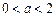 时,∵
时,∵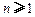 ,
,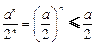 ,∴
,∴ ,∴
,∴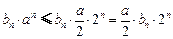 .
.∴
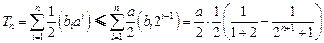 .
.取
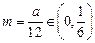 ,若存在
,若存在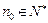 ,当
,当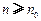 时,
时,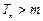 ,则
,则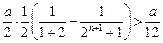 .
.∴
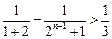 矛盾. 故不存在
矛盾. 故不存在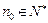 ,当
,当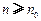 时,
时,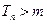 .不满足条件.
.不满足条件.综上所述:只有
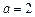 时满足条件,故
时满足条件,故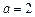 .…………14′
.…………14′同答案

练习册系列答案
相关题目
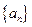 满足递推关系式:
满足递推关系式: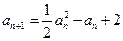 ,
,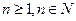 .
.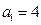 ,证明:(ⅰ)当
,证明:(ⅰ)当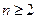 时,有
时,有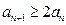 ;(ⅱ)当
;(ⅱ)当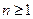 时,有
时,有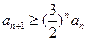 .
.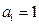 ,证明:当
,证明:当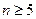 时,有
时,有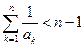 .
.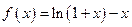 ,数列
,数列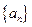 满足:
满足: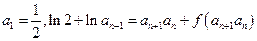 .
.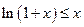 ;
;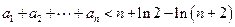
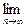 xn
xn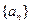 是各项都为正数的数列,
是各项都为正数的数列,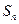 为其前
为其前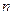 项的和,且
项的和,且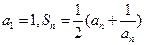
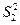 ,
,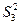 的值;(II)求数列
的值;(II)求数列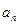 ;(III)求证:
;(III)求证: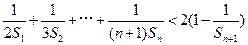
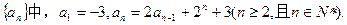
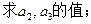 (2)设
(2)设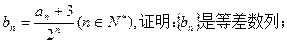
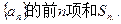

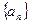 的前
的前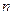 项和为
项和为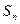 ,公差
,公差
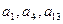 成等比数列.
成等比数列.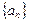 的通项公式;
的通项公式;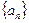 中依次取出第2项、第4项、第8项,……,
中依次取出第2项、第4项、第8项,……,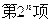 ,……,按原来顺序组成一个新数列
,……,按原来顺序组成一个新数列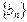 ,记该数列的前
,记该数列的前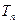 ,求
,求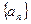 共有
共有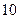 项,其奇数项之和为
项,其奇数项之和为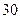 ,则其公差是 .
,则其公差是 .