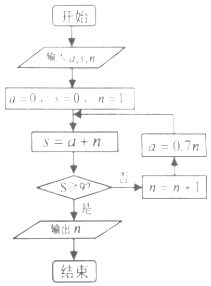
题目内容
【题目】抛物线y2=2x与直线y=x﹣4围成的平面图形面积( )
A.18
B.16
C.20
D.14
【答案】A
【解析】解:方法一:根据题目信息,作出图形,如图所示: 
联立 ![]() ,解得:
,解得: ![]() ,或
,或 ![]() ,则所求的面积为S=
,则所求的面积为S= ![]()
![]() dx+
dx+ ![]() (
( ![]() ﹣x+4)dx.
﹣x+4)dx.
∵[ ![]()
![]() ]′=
]′= ![]() ,
,
∴S=[ ![]()
![]() ]
] ![]() +[
+[ ![]()
![]() ﹣
﹣ ![]() +4x]
+4x] ![]() =18
=18
故抛物线y2=2x与直线y=x﹣4所围成的图形的面积是18,
故选A.
方法二:根据题目信息,作出图形,如图所示:
联立 ![]() ,解得:
,解得: ![]() ,或
,或 ![]() ,
,
则所求的面积为S= ![]() (y+4﹣
(y+4﹣ ![]() )dy=(
)dy=( ![]() y2+4y﹣
y2+4y﹣ ![]() )
) ![]() =(8+16﹣
=(8+16﹣ ![]() )=18,
)=18,
故选A.
【考点精析】根据题目的已知条件,利用定积分的概念的相关知识可以得到问题的答案,需要掌握定积分的值是一个常数,可正、可负、可为零;用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目