题目内容
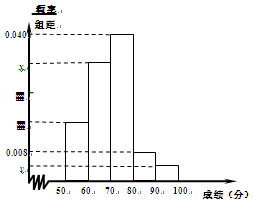
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |
、
(Ⅰ)写出
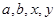 的值;
的值;(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动,设
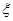 表示所抽取的2名同学中来自第5组的人数,求
表示所抽取的2名同学中来自第5组的人数,求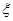 的分布列及其数学期望.
的分布列及其数学期望.
(Ⅰ)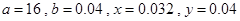 ;
;
(Ⅱ)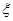


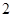
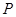

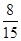

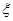 的分布列为
的分布列为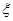


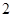
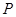

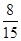

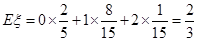 .
.
解析试题分析:(Ⅰ)由频率计算公式易得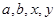 的值;(Ⅱ)可以利用古典概型来计算相应概率,从而得
的值;(Ⅱ)可以利用古典概型来计算相应概率,从而得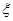 的分布列,最后利用公式求数学期望.
的分布列,最后利用公式求数学期望.
试题解析:(Ⅰ)由题意可知,样本总数为: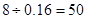

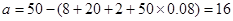

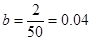
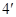
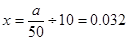

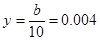
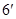
(Ⅱ)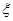 的可能取值为
的可能取值为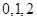 ,
,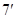
则 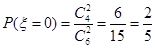 ,
, 
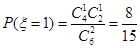 ,
, 
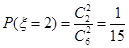 .
. 
所以,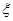 的分布列为
的分布列为
所以,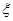


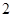
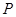

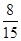

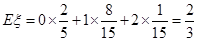 .
. 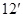
考点:1、概率与统计;2、离散型随机变量分布列;3、离散型随机变量数学期望.

 高中必刷题系列答案
高中必刷题系列答案某年青教师近五年内所带班级的数学平均成绩统计数据如下:
年份 年 年 | 2009 | 2010 | 2011 | 2012 | 2013 |
平均成绩 分 分 | 97 | 98 | 103 | 108 | 109 |
 ,并判断它们之间是正相关还是负相关。
,并判断它们之间是正相关还是负相关。(2)利用(1)中所求出的直线方程预测该教师2014年所带班级的数学平均成绩.

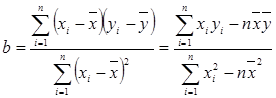


某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | | | | b | | |
| 频率 | a | 0.25 | | | | |

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩在[100,130)范围内的学生中随机选4人,
设其中成绩在[100,110)内的人数为X,求X的分布列及数学期望.
从某学校高三年级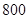 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组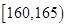 ; 第八组
; 第八组 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图. 
(1)根据已知条件填写下面表格:
| 组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 样本数 | | | | | | | | |
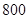 名学生中身高在
名学生中身高在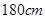 以上(含
以上(含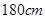 )的人数;
)的人数;(3)在样本中,若第二组有
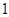 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有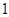 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少? 某校高三有甲、乙两个班,在某次数学测试中,每班各抽取5份试卷,所抽取的平均得分相等(测试满分为100分),成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)学校从甲班的5份试卷中任取两份作进一步分析,在抽取的两份样品中,求至多有一份得分在
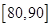 之间的概率.
之间的概率. 某高中在校学生2000人,高一年级与高二年级人数相同并且都比高三年级多1人,为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
| | 高一年级 | 高二年级 | 高三年级 |
| 跑步 |  | 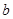 | 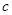 |
| 跳绳 |  |  | 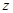 |
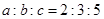 ,全校参与跳绳的人数占总人数的
,全校参与跳绳的人数占总人数的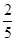 ,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人.
,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人. 某服装商场为了了解毛衣的月销售量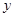 (件)与月平均气温
(件)与月平均气温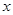 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温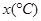 | 17 | 13 | 8 | 2 |
月销售量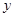 (件) (件) | 24 | 33 | 40 | 55 |
(2) 求线性回归方程
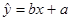 ;
;(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.(
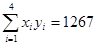 ,
,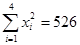 )
)  人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图: ,求
,求 .
.

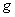 ,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:
,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位: