题目内容
某校高三有甲、乙两个班,在某次数学测试中,每班各抽取5份试卷,所抽取的平均得分相等(测试满分为100分),成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)学校从甲班的5份试卷中任取两份作进一步分析,在抽取的两份样品中,求至多有一份得分在
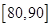 之间的概率.
之间的概率.
(1) (2)
(2)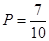 .
.
解析试题分析:(1)平均数公式为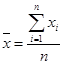 ;(2)列举出从甲班的5份试卷中任取2份的结果10种,至多有一份得分在
;(2)列举出从甲班的5份试卷中任取2份的结果10种,至多有一份得分在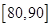 之间的结果7种,则概率为
之间的结果7种,则概率为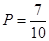 .
.
试题解析:(1)依题意得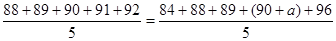 2分
2分
解得 4分
4分
(2)从甲班的5份试卷中任取2份的所有结果有:(88,89),(88,90),(88,91),(88,92),(89,90),
(89,91),(89,92),(90,91),(90,92),(91,92) 6分
共10种 7分
其中至多有一份得分在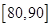 之间的所有结果有:(88,91),(88,92),(89,91),(89,92),(90,91),(90,92),(91,92) 9分
之间的所有结果有:(88,91),(88,92),(89,91),(89,92),(90,91),(90,92),(91,92) 9分
共7种 10分
所以在抽取的样品中,至多有一份得分在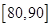 之间的概率
之间的概率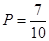 11分
11分
答:在抽取的样品中,至多有一份得分在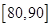 之间的概率
之间的概率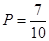 12分
12分
考点:等可能事件,茎叶图.

 阅读快车系列答案
阅读快车系列答案某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |
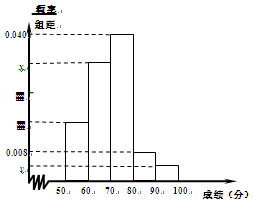
、
(Ⅰ)写出
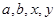 的值;
的值;(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动,设
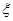 表示所抽取的2名同学中来自第5组的人数,求
表示所抽取的2名同学中来自第5组的人数,求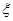 的分布列及其数学期望.
的分布列及其数学期望. 某主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示
| | 积极参加班级工作 | 不太主动参加班级工作 |
| 学习积极性高 | 18 | 7 |
| 学习积极性一般 | 6 | 19 |
(II)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由
附:
P(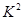 ≥k) ≥k) | 0.050 | 0.010 | 0.001 | 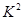 = =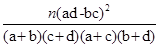 |
| k | 3.841 | 6.635 | 10.828 |
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
| | 患病 | 未患病 | 总计 |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
 P(Y=0).
P(Y=0).(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次, 若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为
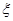 .,求
.,求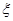 的期望E(
的期望E(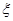 )和方差D(
)和方差D(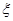 ).
).参考公式:
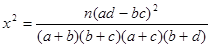 (其中
(其中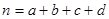 )
)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
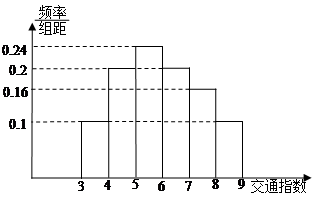
 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.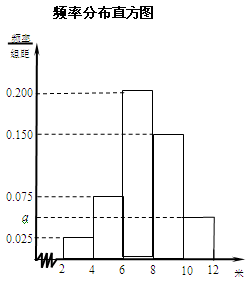
 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;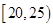 ,第2组
,第2组 ,第3组
,第3组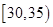 ,第4组
,第4组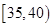 ,第5组
,第5组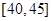 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
 、第2组
、第2组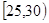 、第3组
、第3组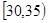 、第4组
、第4组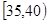 、第5组
、第5组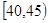 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
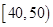 ,
,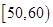 ,
,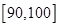 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.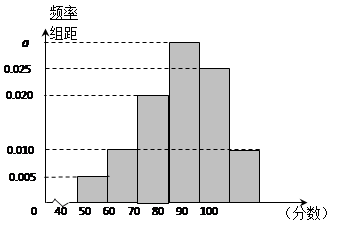
 的值;
的值;