题目内容
在锐角△ABC中,角A、B、C所对的边长分别为a、b、c.向量m=(1,cosB),n=(sinB,-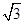 ),且m⊥n.
),且m⊥n.
(1)求角B的大小;
(2)若△ABC面积为10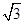 ,b=7,求此三角形周长.
,b=7,求此三角形周长.
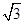 ),且m⊥n.
),且m⊥n.(1)求角B的大小;
(2)若△ABC面积为10
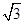 ,b=7,求此三角形周长.
,b=7,求此三角形周长.(1)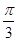 (2)20
(2)20
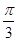 (2)20
(2)20(1)m·n=sinB-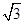 cosB,∵m⊥n,∴m·n=0,
cosB,∵m⊥n,∴m·n=0,
∴sinB-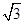 cosB=0.∵△ABC为锐角三角形,∴cosB≠0,
cosB=0.∵△ABC为锐角三角形,∴cosB≠0,
∴tanB=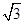 .∵0<B<
.∵0<B<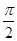 ,∴B=
,∴B=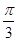 .
.
(2)∵S△ABC=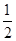 acsinB=
acsinB=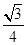 ac,由题设
ac,由题设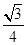 ac=10
ac=10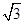 ,得ac=40.由72=a2+c2-2accosB,得49=a2+c2-ac,∴(a+c)2=(a2+c2-ac)+3ac=49+120=169.∴a+c=13,
,得ac=40.由72=a2+c2-2accosB,得49=a2+c2-ac,∴(a+c)2=(a2+c2-ac)+3ac=49+120=169.∴a+c=13,
∴三角形周长是20.
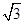 cosB,∵m⊥n,∴m·n=0,
cosB,∵m⊥n,∴m·n=0,∴sinB-
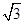 cosB=0.∵△ABC为锐角三角形,∴cosB≠0,
cosB=0.∵△ABC为锐角三角形,∴cosB≠0,∴tanB=
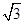 .∵0<B<
.∵0<B<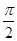 ,∴B=
,∴B=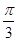 .
.(2)∵S△ABC=
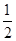 acsinB=
acsinB=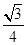 ac,由题设
ac,由题设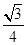 ac=10
ac=10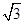 ,得ac=40.由72=a2+c2-2accosB,得49=a2+c2-ac,∴(a+c)2=(a2+c2-ac)+3ac=49+120=169.∴a+c=13,
,得ac=40.由72=a2+c2-2accosB,得49=a2+c2-ac,∴(a+c)2=(a2+c2-ac)+3ac=49+120=169.∴a+c=13,∴三角形周长是20.

练习册系列答案
相关题目
 中,角
中,角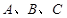 对边分别是
对边分别是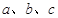 ,满足
,满足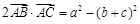 .
.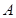 的大小;
的大小; 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的大小.
的大小. 中,角
中,角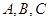 所对的边分别为
所对的边分别为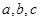 ,已知
,已知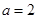 ,
,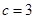 ,
,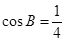 ,求
,求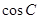 .
.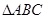 中
中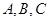 的对边分别是
的对边分别是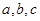 ,面积
,面积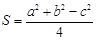 ,则
,则 的大小是( )
的大小是( ) 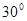
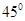
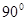
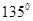 、
、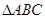 中,三边
中,三边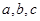 与面积
与面积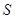 的关系式为
的关系式为 ,则角
,则角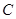 为( )
为( )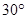

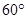

 km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离. ,-1),n=(cos A,sin A).若m⊥n,且acos C+ccos A=bsin B,则角C的大小为________.
,-1),n=(cos A,sin A).若m⊥n,且acos C+ccos A=bsin B,则角C的大小为________. ,点D在BC边上,∠ADC=75°,则AD的长为________.
,点D在BC边上,∠ADC=75°,则AD的长为________.