题目内容
已知a，b，c分别为△ABC的三个内角A，B，C的对边，向量m＝(
，－1)，n＝(cos A，sin A)．若m⊥n，且acos C＋ccos A＝bsin B，则角C的大小为________．
，－1)，n＝(cos A，sin A)．若m⊥n，且acos C＋ccos A＝bsin B，则角C的大小为________．
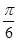
∵m⊥n，∴cos A－sin A＝0，∴2sin
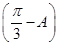＝0，∴A＝
.
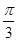由余弦定理得，
acos C＋ccos A＝a·
＋c·
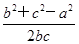＝b.
又∵acos C＋ccos A＝bsin B，∴sin B＝1，∴B＝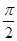
，∴C＝.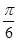
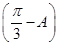cos A－sin A＝0，∴2sin＝0，∴A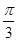＝.由余弦定理得，
acos C＋ccos A＝a·
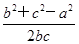＋c·＝b.又∵acos C＋ccos A＝bsin B，∴sin B＝1，∴B＝
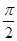，∴C＝.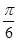
练习册系列答案
相关题目
的最小值及单调减区间；
中，
分别是角
的对边，且
，
，
，且
，求
,c的值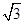
)，且m⊥n.
,BC=2,∠B=60°,则△ABC的面积等于 . 
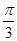，3a＝2c＝6，则b的值为( )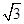
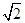
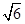－1
.
-cos 2A的值.
,求bc的最大值.
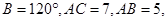，则
．