题目内容

【题目】设函数f（x）=（x﹣a）（x﹣b）（x﹣c）（其中a＞1，b＞1），x=0是f（x）的一个零点，曲线y=f（x）在点（1，f（1））处的切线平行于x轴，则a+b的最小值为 ．

【答案】6
【解析】解：函数f（x）=（x﹣a）（x﹣b）（x﹣c）（其中a＞1，b＞1），x=0是f（x）的一个零点，

可得f（0）=0，即﹣abc=0，可得c=0，

即f（x）=x（x﹣a）（x﹣b）=x3﹣（a+b）x2+abx，

f′（x）=3x2﹣2（a+b）x+ab，

由曲线y=f（x）在点（1，f（1））处的切线平行于x轴，

可得3﹣2（a+b）+ab=0，

即3+ab=2（a+b），

由a＞1，b＞1，可得ab≤（ ）2，

当且仅当a=b取得等号，

即有2（a+b）≤3+（ ）2，

解得a+b≥6或a+b≤2（舍去），

则当且仅当a=b=3时，取得最小值6．

所以答案是：6．

练习册系列答案
相关题目

【题目】设关于的一元二次方程．

（1）若是从0，1，2，3，4五个数中任取的一个数，是从0，1，2三个数中任取的一个数，求上述方程有实根的概率；

（2）若是从区间上任取的一个数，是从区间上任取的一个数，求上述方程有实根的概率．

【题目】给出下列四个结论： ① （x2+sinx）dx=18，则a=3；
②用相关指数R2来刻画回归效果，R2的值越大，说明模型的拟合效果越差；
③若f（x）是定义在R上的奇函数，且满足f（x+2）=﹣f（x），则函数f（x）的图象关于x=1对称；
④已知随机变量ξ服从正态分布N（1，σ2），P（ξ≤4）=0.79，则P（ξ＜﹣2）=0.21；
其中正确结论的序号为 ．

【题目】如图为中国传统智力玩具鲁班锁，起源于古代汉族建筑中首创的榫卯结构，这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合，外观看是严丝合缝的十字立方体，其上下、左右、前后完全对称，六根完全相同的正四棱柱分成三组，经90°榫卯起来．现有一鲁班锁的正四棱柱的底面正方形边长为1，欲将其放入球形容器内（容器壁的厚度忽略不计），若球形容器表面积的最小值为30π，则正四棱柱体的高为（ ）
A.
B.
C.
D.5

【题目】已知函数f（x）=（x﹣3）ex+ax，a∈R． （Ⅰ）当a=1时，求曲线f（x）在点（2，f（2））处的切线方程；
（Ⅱ）当a∈[0，e）时，设函数f（x）在（1，+∞）上的最小值为g（a），求函数g（a）的值域．

【题目】已知函数f（x）=xlnx，g（x）=x+ （x＞0）都在x=x0处取得最小值．
（1）求f（x0）﹣g（x0）的值．
（2）设函数h（x）=f（x）﹣g（x），h（x）的极值点之和落在区间（k，k+1），k∈N，求k的值．

【题目】某公司为评估两套促销活动方案（方案1运作费用为5元/件；方案2的运作费用为2元/件），在某地区部分营销网点进行试点（每个试点网点只采用一种促销活动方案），运作一年后，对比该地区上一年度的销售情况，制作相应的等高条形图如图所示．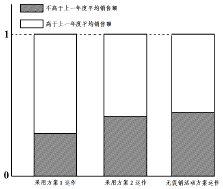
（1）请根据等高条形图提供的信息，为该公司今年选择一套较为有利的促销活动方案（不必说明理由）；
（2）已知该公司产品的成本为10元/件（未包括促销活动运作费用），为制定本年度该地区的产品销售价格，统计上一年度的8组售价xi（单位：元/件，整数）和销量yi（单位：件）（i=1，2，…，8）如下表所示：

售价x

33

35

37

39

41

43

45

47

销量y

840

800

740

695

640

580

525

460

①请根据下列数据计算相应的相关指数R2 ， 并根据计算结果，选择合适的回归模型进行拟合；
②根据所选回归模型，分析售价x定为多少时？利润z可以达到最大．

49428.74

11512.43

175.26

124650

（附：相关指数 ）

【题目】设{an}是首项为1，公差为2的等差数列，{bn}是首项为1，公比为q的等比数列．记cn=an+bn ， n=1，2，3，…．
（1）若{cn}是等差数列，求q的值；
（2）求数列{cn}的前n项和Sn ．

【题目】已知函数 ．
（I）若α是第二象限角，且 的值；
（Ⅱ）求函数f（x）在[0，2π]上的单调递增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网