题目内容
(1)如图3-3,某人投标投中圆的概率是多少(投在正方形外面或边缘不算)?
(2)同(1)中图形,利用随机模拟的方法近似计算正方形内切圆的面积,并估计π的近似值.
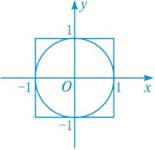
图3-3
(2)同(1)中图形,利用随机模拟的方法近似计算正方形内切圆的面积,并估计π的近似值.

图3-3
(1)这是一个面积型几何概率问题,圆与正方形面积之比为所求概率,为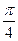 .
.
(2)①利用计算机产生两组[0,1]上的均匀随机数,a1=RAND,b1=RAND;
②进行平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2,得到两组[-1,1]上的均匀随机数;
③统计试验总次数N和落在圆内的点数N1;
④计算频率fn(A)=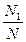 ,即为所求概率的近似值;
,即为所求概率的近似值;
⑤设圆的面积为S,由几何概率公式得点落在阴影部分的概率为P=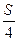 .
.
∴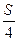 =
=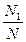 .∴S≈
.∴S≈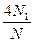 .
.
又S圆=πr2=π,∴π=S≈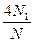 ,即为圆周率的近似值.
,即为圆周率的近似值.
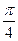 .
.(2)①利用计算机产生两组[0,1]上的均匀随机数,a1=RAND,b1=RAND;
②进行平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2,得到两组[-1,1]上的均匀随机数;
③统计试验总次数N和落在圆内的点数N1;
④计算频率fn(A)=
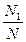 ,即为所求概率的近似值;
,即为所求概率的近似值;⑤设圆的面积为S,由几何概率公式得点落在阴影部分的概率为P=
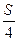 .
.∴
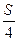 =
=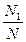 .∴S≈
.∴S≈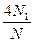 .
.又S圆=πr2=π,∴π=S≈
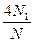 ,即为圆周率的近似值.
,即为圆周率的近似值.由几何概型及随机模拟试验过程求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


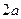 的平行线,把一枚半径
的平行线,把一枚半径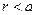 的硬币任意掷在这个平面上,求硬币不与任何一条平行线相碰的概率。
的硬币任意掷在这个平面上,求硬币不与任何一条平行线相碰的概率。
