题目内容
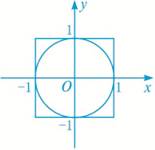
利用随机模拟的方法近似计算边长为2的正方形内切圆面积,并估计π的近似值.
(1)利用计算机产生两组[0,1]上的均匀随机数,a1=RAND,b1=RAND;
(2)进行平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2,得到两组[-1,1]上的均匀随机数;
(3)统计试验总次数N和落在阴影内的点数N1(满足条件a2+b2≤1的点(a,b)的个数);
(4)计算频率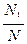 ,即为点落在圆内的概率的近似值;
,即为点落在圆内的概率的近似值;
(5)设圆的面积为S,由几何概率公式得点落在阴影部分的概率为P=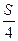 .
.
∴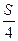 =
=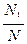 .
.
∴S≈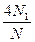 ,即为圆的面积的近似值.
,即为圆的面积的近似值.
又S圆=πr2=π,∴π=S≈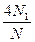 ,即为圆周率的近似值.
,即为圆周率的近似值.
(2)进行平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2,得到两组[-1,1]上的均匀随机数;
(3)统计试验总次数N和落在阴影内的点数N1(满足条件a2+b2≤1的点(a,b)的个数);
(4)计算频率
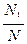 ,即为点落在圆内的概率的近似值;
,即为点落在圆内的概率的近似值;(5)设圆的面积为S,由几何概率公式得点落在阴影部分的概率为P=
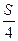 .
.∴
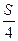 =
=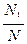 .
.∴S≈
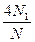 ,即为圆的面积的近似值.
,即为圆的面积的近似值.又S圆=πr2=π,∴π=S≈
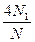 ,即为圆周率的近似值.
,即为圆周率的近似值.用随机模拟的方法可以估算点落在圆内的概率,由几何概率公式可得点落在圆内的概率为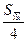 ,这样就可以计算圆的面积,应用圆面积公式可得S圆=πr2=π,所以上面求得的S圆的近似值即为π的近似值.
,这样就可以计算圆的面积,应用圆面积公式可得S圆=πr2=π,所以上面求得的S圆的近似值即为π的近似值.
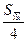 ,这样就可以计算圆的面积,应用圆面积公式可得S圆=πr2=π,所以上面求得的S圆的近似值即为π的近似值.
,这样就可以计算圆的面积,应用圆面积公式可得S圆=πr2=π,所以上面求得的S圆的近似值即为π的近似值.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
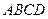 中,
中,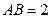 ,
,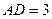 ,如果向该矩形内随机投一点
,如果向该矩形内随机投一点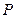 ,
,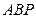 与△
与△ 面积都不小于
面积都不小于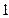 的概率
的概率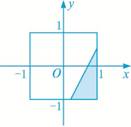
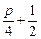 =0有实根的概率.
=0有实根的概率.
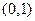 中随机地取出两个数,求两数之和小于
中随机地取出两个数,求两数之和小于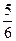 的概率。
的概率。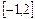 上随机取一个数
上随机取一个数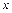 ,则
,则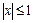 的概率为. ________________________
的概率为. ________________________