题目内容
过点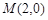 作斜率为1的直线l,交抛物线
作斜率为1的直线l,交抛物线 于A、B两点,则|AB|= .
于A、B两点,则|AB|= .
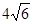
解析试题分析:直线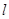 的方程为:
的方程为: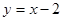 ,和抛物线方程
,和抛物线方程 联立,消去
联立,消去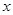 可得:
可得: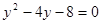 ,设点
,设点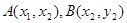 ,由弦长公式:
,由弦长公式:
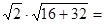
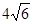 .
.
考点:1、直线的方程;2、弦长公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
过点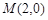 作斜率为1的直线l,交抛物线
作斜率为1的直线l,交抛物线 于A、B两点,则|AB|= .
于A、B两点,则|AB|= .
解析试题分析:直线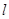 的方程为:
的方程为: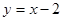 ,和抛物线方程
,和抛物线方程 联立,消去
联立,消去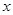 可得:
可得: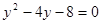 ,设点
,设点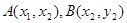 ,由弦长公式:
,由弦长公式:
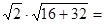
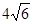 .
.
考点:1、直线的方程;2、弦长公式.

 阅读快车系列答案
阅读快车系列答案