题目内容
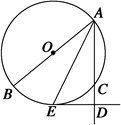
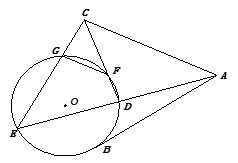
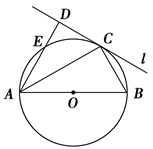
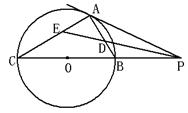
如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.
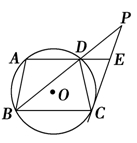
(1)求证:AB2=DE·BC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.

(1)求证:AB2=DE·BC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
(1)见解析(2)

(1)∵AD∥BC,∴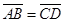 .∴AB=CD,∠EDC=∠BCD.
.∴AB=CD,∠EDC=∠BCD.
又PC与⊙O相切,∴∠ECD=∠DBC.∴△CDE∽△BCD.∴ .
.
∴CD2=DE·BC,即AB2=DE·BC.
(2)由(1)知,DE=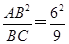 =4,∵AD∥BC,∴△PDE∽△PBC,∴
=4,∵AD∥BC,∴△PDE∽△PBC,∴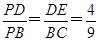 又∵PB-PD=9,∴PD=
又∵PB-PD=9,∴PD=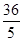 ,PB=
,PB=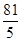 .∴PC2=PD·PB=
.∴PC2=PD·PB=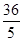 ·
·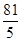 =
=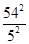 .∴PC=
.∴PC= .
.
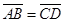 .∴AB=CD,∠EDC=∠BCD.
.∴AB=CD,∠EDC=∠BCD.又PC与⊙O相切,∴∠ECD=∠DBC.∴△CDE∽△BCD.∴
 .
.∴CD2=DE·BC,即AB2=DE·BC.
(2)由(1)知,DE=
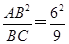 =4,∵AD∥BC,∴△PDE∽△PBC,∴
=4,∵AD∥BC,∴△PDE∽△PBC,∴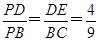 又∵PB-PD=9,∴PD=
又∵PB-PD=9,∴PD=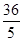 ,PB=
,PB=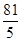 .∴PC2=PD·PB=
.∴PC2=PD·PB=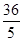 ·
·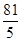 =
=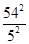 .∴PC=
.∴PC= .
.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 是
是 的一条切线,切点为
的一条切线,切点为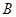 ,
,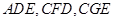 都是
都是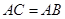 .
.
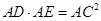 ;
;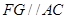 .
. 为圆
为圆 的直径,
的直径,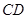 为垂直于
为垂直于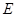 ,弦
,弦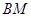 与
与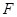 .
.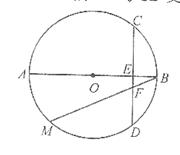
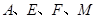 四点共圆;
四点共圆;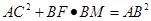 .
.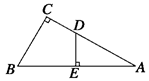

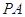 与圆
与圆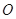 相切于点
相切于点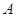 ,经过点
,经过点 交圆
交圆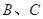 ,
,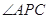 的平分线分别交
的平分线分别交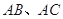 于点
于点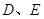 .
.
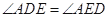 ;
;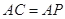 ,求
,求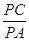 的值.
的值.