题目内容
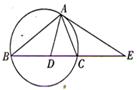
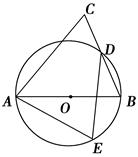
如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为________.


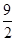
由切割线定理,得CD2=BD·AD.
因为CD=6,AB=5,则36=BD(BD+5),
即BD2+5BD-36=0,
即(BD+9)(BD-4)=0,所以BD=4.
因为∠A=∠BCD,所以△ADC∽△CDB,于是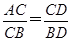 .
.
所以AC=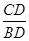 ·BC=
·BC=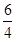 ×3=
×3=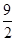 .
.
因为CD=6,AB=5,则36=BD(BD+5),
即BD2+5BD-36=0,
即(BD+9)(BD-4)=0,所以BD=4.
因为∠A=∠BCD,所以△ADC∽△CDB,于是
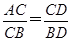 .
.所以AC=
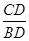 ·BC=
·BC=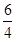 ×3=
×3=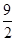 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
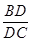 =
=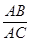 .
.
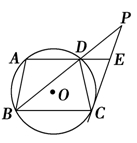
 四点在同一圆上,
四点在同一圆上, 与
与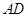 的延长线交于点
的延长线交于点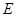 ,点
,点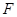 在
在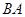 的延长线上.
的延长线上.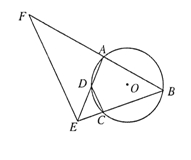
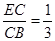 ,
,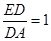 ,求
,求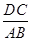 的值;
的值;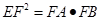 ,证明:
,证明: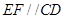 .
.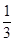 AC,AE=
AC,AE=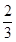 AB,BD,CE相交于点F.
AB,BD,CE相交于点F.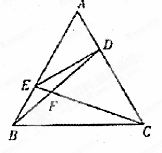
 的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,
的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,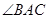 的平分线与BC和圆
的平分线与BC和圆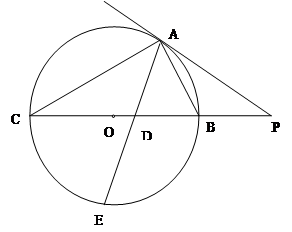
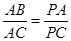 ;
;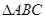 的外接圆的切线
的外接圆的切线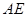 与
与 的延长线相交于点
的延长线相交于点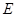 ,
,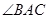 的平分线与
的平分线与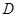 ,若
,若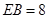 ,
,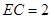 ,则
,则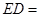 ______.
______.