Question

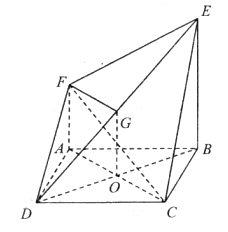
【题目】如图，四边形ABCD是边长为2的正方形，平面ABCD⊥平面ABEF，AF∥BE，AB⊥BE，AB＝BE＝2，AF＝1.

（Ⅰ）求证：AC⊥平面BDE；

（Ⅱ）求证：AC∥平面DEF；

（Ⅲ）求三棱锥A—DEF的体积.

Answer 1

【答案】(Ⅰ)证明见解析；(Ⅱ)证明见解析；(Ⅲ) .

【解析】试题分析：

（Ⅰ）由面面垂直的性质可得BE⊥平面ABCD，BE⊥AC，且AC⊥BD.结合线面垂直的判断定理有AC⊥平面BDE.

（Ⅱ）设AC∩BD＝O，很明显O为BD中点，设G为DE的中点，连结OG，FG，结合几何关系可证得四边形AOGF为平行四边形，故AC∥FG，由线面平行的判断定理可得AC∥平面DEF.

（Ⅲ）由（Ⅰ）可知BE⊥平面ABCD，则AF⊥AD.又AB⊥AD，故AD⊥平面ABEF，转化顶点有： .

试题解析：

（Ⅰ）因为平面ABCD⊥平面ABEF，

平面ABCD∩平面ABEF＝AB，且AB⊥BE，所以BE⊥平面ABCD，

因为平面ABCD，所以BE⊥AC，

又因为四边形ABCD为正方形，所以AC⊥BD.

因为BD∩BE＝B，所以AC⊥平面BDE.

（Ⅱ）设AC∩BD＝O，

因为四边形ABCD为正方形，

所以O为BD中点，

设G为DE的中点，连结OG，FG，

则OG∥BE，且，

由已知AF∥BE，且，

则AF∥OG，且AF＝OG.

所以四边形AOGF为平行四边形，

所以AO∥FG，即AC∥FG，

因为平面DEF， 平面DEF，

所以AC∥平面DEF.

（Ⅲ）由（Ⅰ）可知BE⊥平面ABCD，

因为AF∥BE，所以AF⊥平面ABCD，

所以AF⊥AB，AF⊥AD.

又因为四边形ABCD为正方形，所以AB⊥AD，

所以AD⊥平面ABEF，

因为AB＝AD＝2AF＝2，

所以

，

故三棱锥的体积为.