题目内容
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量y(单位:万只)与相成年份x(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数z(单位:个)关于x的回归方程![]() .
.

(1)根据表中的数据和所给统计量,求y关于x的线性回归方程(参考统计量:![]() );
);
(2)试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据题设中的数据,求得![]() ,
,![]() ,利用公式
,利用公式![]() ,进而得到
,进而得到![]() ,即可得到回归直线的方程;
,即可得到回归直线的方程;
(2)求得第![]() 年山羊养殖的只数
年山羊养殖的只数![]() ,①代入
,①代入![]() ,即可得到第一年的山羊的养殖只数;②根据题意,得
,即可得到第一年的山羊的养殖只数;②根据题意,得![]() ,求得
,求得![]() ,即可得到结论
,即可得到结论
(1)设![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
则![]() ,
,
![]() ,
,
则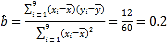 ,所以
,所以![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() 。
。
(2)估计第![]() 年山羊养殖的只数
年山羊养殖的只数![]() ,
,
①第1年山羊养殖的只数为![]() ,故该县第一年养殖山羊约
,故该县第一年养殖山羊约![]() 万只;
万只;
②由题意,得![]() ,整理得
,整理得![]() ,
,
解得![]() 或
或![]() (舍去)
(舍去)
所以到第10年该县山羊养殖的数量相比第1年缩小了。

【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用![]() 配方、
配方、![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(2)已知用![]() 配方生产的一件产品的利润(单位:元)与其质量指标值
配方生产的一件产品的利润(单位:元)与其质量指标值![]() 的关系为
的关系为 ,估计用
,估计用![]() 配方生产的一件产品的利润大于
配方生产的一件产品的利润大于![]() 的概率,并求用
的概率,并求用![]() 配方生产的上述
配方生产的上述![]() 件产品的平均利润.
件产品的平均利润.
