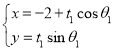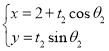题目内容
【题目】已知椭圆![]() ,过点
,过点![]() 的两条不同的直线与椭圆E分别相交于A,B和C,D四点,其中A为椭圆E的右顶点.
的两条不同的直线与椭圆E分别相交于A,B和C,D四点,其中A为椭圆E的右顶点.
(1)求以AB为直径的圆的方程;
(2)设以AB为直径的圆和以CD为直径的圆相交于M,N两点,探究直线MN是否经过定点,若经过定点,求出定点坐标;若不经过定点,请说明理由.
【答案】(1)![]() ;(2)经过定点,
;(2)经过定点,![]() .
.
【解析】
(1)由已知得AB方程:![]() ,与椭圆方程联立可求出
,与椭圆方程联立可求出![]() ,则可求出以AB为直径的圆的圆心和半径,进而可求出圆的方程;
,则可求出以AB为直径的圆的圆心和半径,进而可求出圆的方程;
(2)当CD斜率存在时,并设CD方程:![]() ,与椭圆方程联立,通过根与系数的关系可得以CD为直径的圆方程,将其与以AB为直径的圆的方程作差,可得直线MN的方程,进而可得直线MN过的定点
,与椭圆方程联立,通过根与系数的关系可得以CD为直径的圆方程,将其与以AB为直径的圆的方程作差,可得直线MN的方程,进而可得直线MN过的定点![]() ,当CD斜率不存在时,直线MN也过的定点
,当CD斜率不存在时,直线MN也过的定点![]() ,进而可得答案.
,进而可得答案.
(1)由已知![]() ,则
,则![]() ,故AB方程:
,故AB方程:![]() ,
,
联立直线AB与椭圆方程,消去y可得:![]() ,得
,得![]() ,即
,即![]() ,
,
从而以AB为直径的圆的圆心为![]() ,半径为
,半径为 ,
,
所以圆的方程为 ,
,
即![]() .;
.;
(2)①当CD斜率存在时,并设CD方程:![]() ,
,
设![]() ,
,![]()
由 ,消去y得:
,消去y得:![]() ,
,
故![]() ,
,![]() ,
,
从而![]() ,
,
![]() ,
,
而以CD为直径的圆方程为:![]() ,
,
即![]() ①,
①,
且以AB为直径的圆方程为![]() ②,
②,
②-①得直线![]() ,
,
即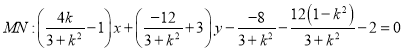
整理得![]() ,
,
可得:![]() ,
,
因为AB与 CD两条直线互异,则![]() ,
,
即![]() ,
,
令![]() ,解得
,解得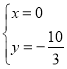 ,即直线MN过定点
,即直线MN过定点![]() ;
;
②当CD斜率不存在时,CD方程:![]() ,知
,知![]() ,
,![]() ,
,
则以CD为直径的圆为![]() ,
,
而以AB为直径的圆方程![]() ,
,
两式相减得MN方程:![]() ,过点
,过点![]() ;
;
综上所述,直线MN过定点![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目