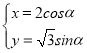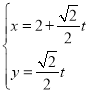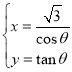题目内容
【题目】在直角坐标系
中，已知曲线
：
（
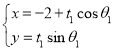为参数），曲线
：
（
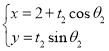为参数），且
，点P为曲线与的公共点.
（1）求动点P的轨迹方程；
（2）在以原点O为极点，x轴的非负半轴为极轴的极坐标系中，直线l的极坐标方程为
，求动点P到直线l的距离的取值范围.
【答案】（1）
（
）.（2）
【解析】
（1）设点
，点P同时满足曲线
与
的方程，消参得，
，
，由
，即可求得点的轨迹方程；
（2）由
，
，将极坐标方程转化为直角坐标方程，动点为圆心在原点，半径为2的圆，先求出圆心到直线
的距离，即可求出动点到直线的取值范围.
解析：（1）设点P的坐标为.
因为点P为曲线与的公共点，所以点P同时满足曲线与的方程.
曲线消去参数可得，曲线消去参数可得.
由，所以
.
所以点P的轨迹方程为（）.
（2）由已知，直线l的极坐标方程
，
根据，可化为直角坐标方程：
.
因为P的轨迹为圆（去掉两点
），
圆心O到直线l的距离为
，
所以点P到直线l的距离的取值范围为.
练习册系列答案
相关题目
