题目内容
7.已知直角三角形的三边长分别为a,b,c(其中c为斜边长),其内切圆半径为t,求证:r=$\frac{a+b-c}{2}$.分析 作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,根据切线的性质得OD=OE=OF=r,再证明四边形CEOF为正方形,所以CE=CF=r,然后根据切线长定理得AE=AD=b-r,BF=BD=a-r,则b-r+a-r=c,所以r=$\frac{a+b-c}{2}$.
解答 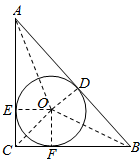 证明:作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,
证明:作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,
∵⊙O为△ABC的内切圆,
∴OD=OE=OF=r,
∵∠ACB=90°,
∴四边形CEOF为正方形,
∴CE=CF=r,
∴AE=AD=b-r,BF=BD=a-r,
∴b-r+a-r=c,
∴r=$\frac{a+b-c}{2}$.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.熟练运用切线的性质.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
17.若圆M在x轴与y轴上截得的弦长总相等,则圆心M的轨迹方程是( )
| A. | x-y=0 | B. | x+y=0 | C. | x2+y2=0 | D. | x2-y2=0 |