题目内容
11.已知A、B、C三点共线,等差数列{an}满足$\overrightarrow{OA}={a}_{4}\overrightarrow{OB}+({a}_{7}+1)\overrightarrow{OC}$,a3-a11+a14=-1.(Ⅰ)求数列{an}的通项an及前n项和Sn;
(Ⅱ)设数列{bn}满足bn=|an|,试求{bn}的前n项和Tn.
分析 (I)利用向量共线定理可得:a4+(a7+1)=1,又a3-a11+a14=-1.利用等差数列的通项公式及其前n项和公式即可得出.
(II)由an≥0,解得$n≤\frac{11}{2}$;当n≤5时,Tn=Sn.当n≥6时,an<0.Tn=2S5-Sn,即可得出.
解答 解:(I)∵A、B、C三点共线,等差数列{an}满足$\overrightarrow{OA}={a}_{4}\overrightarrow{OB}+({a}_{7}+1)\overrightarrow{OC}$,
∴a4+(a7+1)=1,
又a3-a11+a14=-1.
∴$\left\{\begin{array}{l}{2{a}_{1}+9d=0}\\{{a}_{1}+5d=-1}\end{array}\right.$,解得a1=9,d=-2.
∴an=11-2n,Sn=-n2+10n.
(II)由an≥0,解得$n≤\frac{11}{2}$;
∴当n≤5时,${T}_{n}={S}_{n}=-{n}^{2}$+10n.
当n≥6时,an<0.
∴Tn=2S5-Sn=n2-10n+50.
∴Tn=$\left\{\begin{array}{l}{-{n}^{2}+10n,n≤5}\\{{n}^{2}-10n+50,n≥6}\end{array}\right.$.
点评 本题考查了等差数列的通项公式及其前n项和公式、递推式的应用、含绝对值的数列求和问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.等比数列{an}满足a2+8a5=0,设Sn是数列{$\frac{1}{{a}_{n}}$}的前n项和,则$\frac{{S}_{5}}{{S}_{2}}$=( )
| A. | -11 | B. | -8 | C. | 5 | D. | 11 |
6.若函数f(x)=log${\;}_{\frac{1}{2}}$(-x2+4x+5)在区间(3m-2,m+2)内单调递增,则实数m的取值为( )
| A. | [$\frac{4}{3},3$] | B. | [$\frac{4}{3},2$] | C. | [$\frac{4}{3},2$) | D. | [$\frac{4}{3},+∞$) |
16.在面积为1的△ABC内部随机选取一点P,则△PBC面积大于$\frac{1}{4}$的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{9}{16}$ |
3.某几何体的三视图如图所示,则该几何体的体积为( )
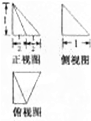

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
20.某校组织一次校外活动,有10名同学参加,其中有6名男生,4名女生,从中随机抽取3名,其中至多有1名女生的概率( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
1.i为虚数单位,复数$\frac{{3i-{i^{2014}}}}{1-i}$的化简结果为( )
| A. | 2+i | B. | 1+2i | C. | -1+2i | D. | -2+i |