题目内容
19.若Sn和Tn分别表示{an}和{bn}的前n项和,对任意正整数n,有an=-n-$\frac{3}{2}$,4Tn=12Sn+13n.(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)设cn=bn+$\frac{5}{4}$,若$\frac{100}{{c}_{1}•{c}_{2}}$+$\frac{100}{{c}_{2}•{c}_{3}}$+…+$\frac{100}{{c}_{n}•{c}_{n+1}}$>11,求n的最小值.
分析 (1)由4Tn=12Sn+13n,可得当n≥2时,4Tn-1=12Sn-1+13(n-1),4bn=12an+13,代入即可得出;
(2)由(1)得:cn=-3n,于是 $\frac{100}{{c}_{n}{c}_{n+1}}$=$\frac{100}{9}(\frac{1}{n}-\frac{1}{n+1})$.利用“裂项求和”与不等式的性质即可得出.
解答 解:(1)∵4Tn=12Sn+13n,
∴当n≥2时,4Tn-1=12Sn-1+13(n-1),4bn=12an+13,
∴${b}_{n}=3{a}_{n}+\frac{13}{4}$=-3n-$\frac{5}{4}$.又b1=-$\frac{17}{4}$也适合上式,
∴数列{bn}的通项公式为bn=-3n-$\frac{5}{4}$.
(2)由(1)得:cn=bn+$\frac{5}{4}$=-3n,
于是 $\frac{100}{{c}_{n}{c}_{n+1}}$=$\frac{100}{9}(\frac{1}{n}-\frac{1}{n+1})$.
∴$\frac{100}{{c}_{1}•{c}_{2}}$+$\frac{100}{{c}_{2}•{c}_{3}}$+…+$\frac{100}{{c}_{n}•{c}_{n+1}}$=$\frac{100}{9}$$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+$…+$(\frac{1}{n}-\frac{1}{n+1})]$=$\frac{100}{9}(1-\frac{1}{n+1})$=$\frac{100}{9}$$•\frac{n}{n+1}$,
令$\frac{100}{9}$$•\frac{n}{n+1}$>11,解得n>99,
∴n的最小值为100.
点评 本题考查了递推式的应用、“裂项求和”与不等式的性质,考查了推理能力与计算能力,属于中档题.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案| A. | (-∞,4-8ln2] | B. | (-∞,$\frac{17}{4}$-8ln2] | C. | (-∞,4+8ln2] | D. | (-∞,$\frac{17}{4}$+8ln2] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
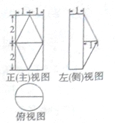
| A. | $\frac{16}{3}$ | B. | 5+$\frac{π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
| A. | a(1+p)5 | B. | a(1+p)6 | C. | $\frac{a}{p}$[(1+p)5-(1+p)] | D. | $\frac{a}{p}$[(1+p)6-(1+p)] |
| x | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| y | 5 | 6 | 12 | 14 | 20 | 23 | 25 |
| A. | 47 | B. | 52 | C. | 55 | D. | 38 |