题目内容
【题目】已知圆
，直线
，在圆
内任取一点
，则到直线的距离大于2的概率为__________．
【答案】
【解析】分析：根据几何概型，求出圆心到直线的距离，利用几何概型的概率公式分别求出对应的测度即可得到结论．
详解：由题意知圆的标准方程为（x﹣1）2+y2=2的圆心是（1，0），
圆心到直线3x﹣4y+12=0的距离是d=
=3，
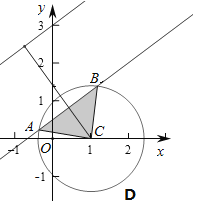
当与3x﹣4y+12=0平行，且在直线下方距离为2的平行直线为3x﹣4y+b=0，
则d=
=2，则|b﹣12|=10，
即b=22（舍）或b=2，此时直线为3x﹣4y+2=0，
则此时圆心到直线3x﹣4y+2=0的距离d=1，即三角形ACB为直角三角形，
当P位于3x﹣4y+2=0时，此时P到直线l的距离大于2，
则根据几何概型的概率公式得到P=
=
故答案为：．
练习册系列答案
走进文言文系列答案
相关题目
【题目】从集市上买回来的蔬菜仍存有残留农药，食用时需要清洗数次，统计表中的
表示清洗的次数，
表示清洗次后
千克该蔬菜残留的农药量（单位：微克）.
|
|
|
|
|
|
|
|
|
|
|
|
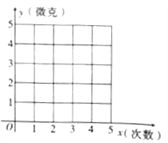
（1）在如图的坐标系中，描出散点图，并根据散点图判断，
哪一个适宜作为清洗次后千克该蔬菜残留的农药量的回归方程类型；（给出判断即可，不必说明理由）
（2）根据判断及下面表格中的数据，建立关于的回归方程；
表中
，
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（3）对所求的回归方程进行残差分析.
附：①线性回归方程中系数计算公式分别为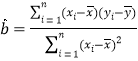
，
；
②
，
说明模拟效果非常好；
③
，
，
，
，
.
