题目内容
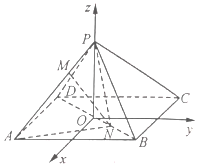
【题目】如图，在空间直角坐标系O﹣xyz中，已知正四棱锥P﹣ABCD的所有棱长均为6，底面正方形ABCD的中心在坐标原点，棱AD，BC平行于x轴，AB，CD平行于y轴，顶点P在z轴的正半轴上，点M，N分别在线段PA，BD上，且
．
（1）求直线MN与PC所成角的大小；
（2）求锐二面角A﹣PN﹣D的余弦值．
【答案】（1）
；（2）
．
【解析】
（1）首先建立空间直角坐标系，然后求出M，N，P，C点坐标，根据点坐标即可求出直线MN与PC所成角的大小；
（2）首先求出平面APN与平面PND的法向量，根据二面角公式即可求出二面角A﹣PN﹣D的余弦值.
解：（1）如图，已知正四棱锥P﹣ABCD的所有棱长均为6，
，
，
，
，
，
设
，
，
由
，得
，
，
即
，所以
，
，
，
由
，得
，
故
，
所
，
，
所以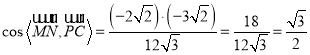
，
所以直线MN与PC所成的角为
；
（2）因为AC
平面PBD，设平面PBD的法向量
，
设平面PAN的法向量为
，
，
，
由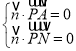
，得
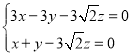，故
，
所以
，
故锐二面角A﹣PN﹣D的余弦值为．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
