Question

【题目】已知函数是定义域为的偶函数，且满足，当时，，则函数在区间上零点的个数为（ ）

A.9B.10C.18D.20

Answer 1

【答案】B

【解析】

由已知可得函数f（x）的周期与对称轴，函数F（x）＝f（x）在区间上零点的个数等价于函数f（x）与g（x）图象在上交点的个数，作出函数f（x）与g（x）的图象如图，数形结合即可得到答案.

函数F（x）＝f（x）在区间上零点的个数等价于函数f（x）与g（x）图象在上交点的个数，

由f（x）＝f （2﹣x），得函数f（x）图象关于x＝1对称，

∵f（x）为偶函数，取x＝x+2，可得f（x+2）＝f（﹣x）＝f（x），得函数周期为2.

又∵当x∈[0，1]时，f（x）＝x，且f（x）为偶函数，∴当x∈[﹣1，0]时，f（x）＝﹣x，

g（x），

作出函数f（x）与g（x）的图象如图：

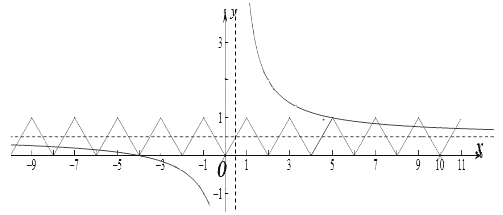
由图可知，两函数图象共10个交点，

即函数F（x）＝f（x）在区间上零点的个数为10.

故选：B.