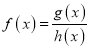题目内容
【题目】已知函数![]()
![]() 且
且![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]()
![]() 且
且![]() ,若
,若![]() ,是否存在实数
,是否存在实数![]() 使函数
使函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)由奇函数的性质![]() ,可求出
,可求出![]() 的值;(2)由
的值;(2)由![]() ,可以求出
,可以求出![]() 的范围,进而可以得到
的范围,进而可以得到![]() 的单调性,然后利用
的单调性,然后利用![]() 奇函数的性质,可以得到
奇函数的性质,可以得到![]() ,从而得到对任意
,从而得到对任意![]() 都有
都有![]() 恒成立,利用二次函数的性质即可求出
恒成立,利用二次函数的性质即可求出![]() 的取值范围;(3)由
的取值范围;(3)由![]() 可求出
可求出![]() ,假设存在实数
,假设存在实数![]() ,构造函数
,构造函数![]() ,则
,则![]() ,对
,对![]() 进行分类讨论,即可判断
进行分类讨论,即可判断![]() 的值。
的值。
(1)因为![]() 的定义域为
的定义域为![]() ,且
,且![]() 为奇函数,
为奇函数,
所以![]() ,解得
,解得![]() .检验:当
.检验:当![]() 时,
时,![]() ,
,
对任意![]() ,都有
,都有![]() ,即
,即![]() 是奇函数,所以
是奇函数,所以![]() 成立。
成立。
(2)由(1)可得![]() ,由
,由![]() 可得
可得![]()
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
则![]() 在
在![]() 单调递减,
单调递减,![]() 在
在![]() 单调递增,
单调递增,
所以![]() 在
在![]() 单调递减,
单调递减,
由![]() 可得
可得![]() ,
,
所以对任意![]() 都有
都有![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() ,解得
,解得![]() .
.
(3)![]() ,
,
由![]() 可得
可得![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() .
.
所以![]() ,易知
,易知![]() 在
在![]() 单调递增.
单调递增.
令![]() ,则
,则![]() ,
,
再令![]() ,则
,则![]()
因为![]() ,
,![]() ,
,
![]() ,
,
所以![]() .因为
.因为![]() 在
在![]() 有意义,
有意义,
所以对任意![]() ,都有
,都有![]() 恒成立,
恒成立,
所以![]() ,即
,即![]()
所以![]() ,所以
,所以![]() .
.
二次函数![]() 图像开口向上,对称轴为直线
图像开口向上,对称轴为直线![]() ,
,
因为![]() ,所以
,所以![]() ,
,
对称轴始终在区间![]() 的左侧
的左侧
所以![]() 在区间
在区间![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
假设存在满足条件的实数![]() ,则:
,则:
若![]() ,则
,则![]() 为减函数,
为减函数,![]() ,
,
即![]() ,所以
,所以![]() ,舍去;
,舍去;
若![]() ,则
,则![]() 为增函数,
为增函数,![]() ,
,
即![]() ,所以
,所以![]() ,舍去.
,舍去.
综上所述,不存在满足条件的实数![]() .
.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案【题目】某校为了解学生一次考试后数学、物理两个科目的成绩情况,从中随机抽取了25位考生的成绩进行统计分析.25位考生的数学成绩已经统计在茎叶图中,物理成绩如下:

(Ⅰ)请根据数据在答题卡的茎叶图中完成物理成绩统计;

(Ⅱ)请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图;
数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
频数 |

(Ⅲ)设上述样本中第i位考生的数学、物理成绩分别为xi,yi(i=1,2,3,…,25).通过对样本数据进行初步处理发现:数学、物理成绩具有线性相关关系,得到:![]() =86,
=86,![]() =64,
=64,![]() (xi-
(xi-![]() )(yi-
)(yi-![]() )=4698,
)=4698,![]() (xi-
(xi-![]() )2=5524,
)2=5524,![]() ≈0.85.求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
≈0.85.求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:![]() =
= ,
,![]() =
=![]() -
-![]() .
.