��Ŀ����
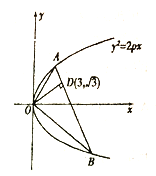
����Ŀ��С�ž�Ӫijһ����Ʒר���꣬��֪������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ�����������ټ��������۵���x��Ԫ/����֮��Ĺ�ϵ����ͼ��һ���߱�ʾ��ְ��ÿ��ÿ�¹���Ϊ1000Ԫ���õ껹Ӧ��������������Ϊÿ��10000Ԫ.

��1����y��ʾΪx�ĺ�����
��2�������ۼ�Ϊÿ��50Ԫʱ���õ�������֧ƽ�⣨������Ϊ�㣩����õ��ְ��������
��3�����õ�ֻ��20��ְ���������۵��۶�Ϊ����Ԫʱ����ר����ɻ�����������ע������=����-֧����
���𰸡���1��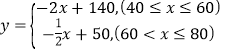 ��2��30��Ա����3�����۵��۶�Ϊ55��70Ԫʱ����ר�������������
��2��30��Ա����3�����۵��۶�Ϊ55��70Ԫʱ����ר�������������
��������
��1�����ô���ϵ�����ֱ������![]() ��
��![]() ʱ�Ľ���ʽ�������ɵ�����������2����õ���ְ��m������������õ�����m�ķ��̣����ɵ�������3��������õ�����ĺ�����ϵʽ�����ݷֶκ�����ֵ���ɵ�������
ʱ�Ľ���ʽ�������ɵ�����������2����õ���ְ��m������������õ�����m�ķ��̣����ɵ�������3��������õ�����ĺ�����ϵʽ�����ݷֶκ�����ֵ���ɵ�������
��1����![]() ʱ����
ʱ����![]() ��
��
������õ�![]() �ں�����ͼ���ϣ�
�ں�����ͼ���ϣ�
��![]() �����
�����![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��
ͬ������![]() ʱ��
ʱ��![]() ��
��
�������ϵʽΪ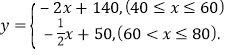
��2����õ���ְ��m����
��x=50ʱ���õ��������Ϊ![]() Ԫ��
Ԫ��
�ָõ����֧��Ϊ1000m+10000Ԫ��
�������40000=1000m+10000,
��ã�m=30.
���Դ�ʱ�õ���30��Ա����
��3�����õ�ֻ��20��ְ����
��������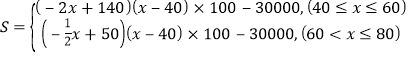
�ٵ�![]() ʱ��
ʱ��![]() ��
��
����x=55ʱ��Sȡ���ֵ15000Ԫ��
�ڵ�![]() ʱ��
ʱ��![]() ��
��
����x=70ʱ��Sȡ���ֵ15000Ԫ��
�ʵ�x=55��x=70ʱ��Sȡ���ֵ15000Ԫ��
�����۵��۶�Ϊ55��70Ԫʱ����ר�������������