题目内容
求曲线y＝x2，直线y＝x，y＝3x围成的图形的面积．
。
解析试题分析：由图知
4分
解方程组
，得交点（1，1），解方程组
，得交点（3，9），由此所围图形面积为：
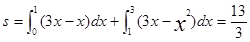。 12分
考点：定积分的计算，定积分的几何意义。
点评：中档题，涉及定积分的几何意义，关键是明确图形的特征，通过研究曲线的交点，确定积分上下限。
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
期末冲刺100分创新金卷完全试卷系列答案题目内容
求曲线y＝x2，直线y＝x，y＝3x围成的图形的面积．
。
解析试题分析：由图知 4分
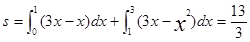解方程组，得交点（1，1），解方程组，得交点（3，9），由此所围图形面积为：。 12分
考点：定积分的计算，定积分的几何意义。
点评：中档题，涉及定积分的几何意义，关键是明确图形的特征，通过研究曲线的交点，确定积分上下限。
期末冲刺100分创新金卷完全试卷系列答案
(
).
时，求函数
的极值； 
，不等式
恒成立，求实数
的取值范围．
)图像上一个最高点坐标为(2,2
)，这个最高点到相邻最低点的图像与x轴交于点(5,0)．
在点
处取得极小值－4，使其导数
的
的取值范围为
，求：
的解析式；
，求
的最大值；
在
上的最大值和最小值.
作曲线
的切线，求此切线的方程. 
在点
处取得极小值－4，使其导数
的
的取值范围为
，求：
的解析式；
，求
的最大值；
．
在点
处的切线方程；
为曲线
的切线，且经过原点，求直线
的方程及切点坐标
.
奇偶性, 并求出函数
的单调区间； 
有零点，求实数
的取值范围.
的图象经过点M(1,4),曲线在点M处的切线恰好与直线
垂直。
的值；
在区间
上单调递增，求
的取值范围.