题目内容
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() .
.

⑴若圆![]() 的半径为2,圆
的半径为2,圆![]() 与
与![]() 轴相切且与圆
轴相切且与圆![]() 外切,求圆
外切,求圆![]() 的标准方程;
的标准方程;
⑵若过原点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) ![]() 或
或![]() (2)
(2) ![]()
【解析】
(1)设出圆![]() 的标准方程为
的标准方程为![]() ,由圆
,由圆![]() 与
与![]() 轴相切,可得
轴相切,可得![]() ,由圆
,由圆![]() 与圆
与圆![]() 外切,可得两圆心距等于半径之和,由此解出
外切,可得两圆心距等于半径之和,由此解出![]() ,
,![]() ,
,![]() 的值,得到圆
的值,得到圆![]() 的标准方程;
的标准方程;
(2)法一:设出![]() 点坐标为
点坐标为![]() ,根据
,根据![]() ,可得到点
,可得到点![]() 坐标,把
坐标,把![]() 、
、![]() 两点坐标代入圆
两点坐标代入圆![]() 方程,解出
方程,解出![]() 点坐标,即可得到直线
点坐标,即可得到直线![]() 的方程;
的方程;
法二:设![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,![]() ,设出直线
,设出直线![]() 的方程,由题求出
的方程,由题求出![]() 的长,利用点到直线的距离即可得求出
的长,利用点到直线的距离即可得求出![]() 值,从而得到直线
值,从而得到直线![]() 的方程
的方程
⑴设圆![]() 的标准方程为
的标准方程为![]() ,故圆心
,故圆心![]() 坐标为
坐标为![]() ,半径
,半径![]() ;
;
因为圆![]() 的半径为2,与
的半径为2,与![]() 轴相切,所以
轴相切,所以![]() ①
①
因为圆![]() 与圆
与圆![]() 外切
外切
所以![]() ,即
,即![]() ②
②
由①②解得![]()
故圆![]() 的标准方程为
的标准方程为![]() 或
或![]()
⑵方法一;设![]()
因为![]() ,所以
,所以![]() 为
为![]() 的中点,从而
的中点,从而![]()
因为![]() ,
,![]() 都在圆
都在圆![]() 上
上
所以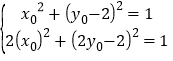
解得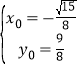 或
或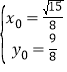
故直线![]() 的方程为:
的方程为:![]()
方法二:设![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,![]()
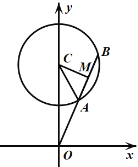
设![]() ,
,![]()
因为![]() ,所以
,所以![]()
在![]() 中,
中,![]() ③
③
在![]() 中,
中,![]() ④
④
由③④解得![]()
由题可知直线![]() 的斜率一定存在,设直线
的斜率一定存在,设直线![]() 的方程为
的方程为![]()
则![]() ,解得
,解得![]()
故直线![]() 的方程为
的方程为![]()

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

