题目内容
【题目】某同学用“五点法”画函数
在某一个周期内的图象时，列出了如表并给出了部分数据:
| 0 |
| π |
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
（1）请根据上表数据，写出函数
的解析式；（直接写出结果即可）
（2）求函数的单调递增区间；
（3）设
，已知函数
在区间
上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />，求t的值以及函数在区间[上的最小值.
【答案】（1）
（2）
，
（3）
，
【解析】
（1）根据表格数据，即可写出
的解析式；
（2）利用正弦函数的单调性即可求解；
（3）根据函数
在区间
上的最大值求出
的值，进而求出最小值即可．
（1）根据表格可得
，所以
；
根据表格可得
，又
，所以
，
故函数的解析式为:.
（2）令
，即
，
所以函数
的单调递增区间为，.
（3）因为
，所以
，故有
.
所以，当
，即
时，在区间上的最小值为
.
当
，即
时，在区间上的最大值为1.
所以t的值为，所以函数
在区间上的最小值为.
直通贵州名校周测月考直通名校系列答案
【题目】已知对某校的100名学生进行不记名问卷调查，内容为一周的课外阅读时长和性别等进行统计，如表：
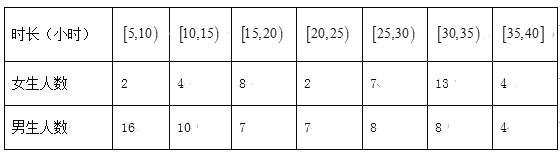
（1）课外阅读时长在20以下的女生按分层抽样的方式随机抽取7人，再从7人中随机抽取2人，求这2人课外阅读时长不低于15的概率；
（2）将课外阅读时长为25以上的学生视为“阅读爱好”者，25以下的学生视为“非阅读爱好”者，根据以上数据完成2×2列联表：
非阅读爱好者 | 阅读爱好者 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.01的前提下，认为学生的“阅读爱好”与性别有关系？
附：
，
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
