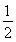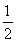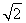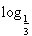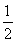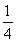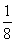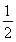题目内容
已知等差数列{an}是递增数列，且满足a4·a7＝15，a3＋a8＝8.
(1)求数列{an}的通项公式；
(2)令bn＝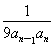
(n≥2)，b1＝
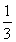，求数列{bn}的前n项和Sn.
（1）
（2）
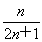
【解析】(1)根据题意：a3＋a8＝8＝a4＋a7，a4·a7＝15，知：a4，a7是方程x2－8x＋15＝0的两根，且a4<a7，解得a4＝3，a7＝5，设数列{an}的公差为d，由a7＝a4＋(7－4)·d，得d＝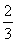
.故等差数列{an}的通项公式为an＝a4＋(n－4)·d＝3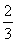＋(n－4)＝.
(2)当n≥2时，bn＝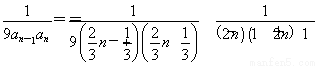
＝
.又b1＝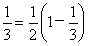
，
∴Sn＝b1＋b2＋…＋bn＝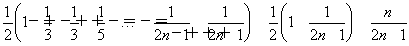
练习册系列答案
名校课堂系列答案
相关题目
