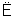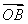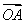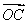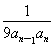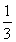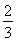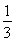题目内容
已知各项均为正数的等比数列{an}的公比为q,且0<q<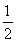 .
.
(1)在数列{an}中是否存在三项,使其成等差数列?说明理由;
(2)若a1=1,且对任意正整数k,ak-(ak+1+ak+2)仍是该数列中的某一项.
(ⅰ)求公比q;
(ⅱ)若bn=-logan+1(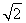 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
(1)不可能(2)(ⅰ)q=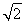 -1(ⅱ)T2011=2012S2011-2011
-1(ⅱ)T2011=2012S2011-2011
【解析】(1)由条件知an=a1qn-1,0<q<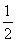 ,a1>0,所以数列{an}是递减数列.若有ak,am,an(k<m<n)成等差数列,则中项不可能是ak(最大),也不可能是an(最小),
,a1>0,所以数列{an}是递减数列.若有ak,am,an(k<m<n)成等差数列,则中项不可能是ak(最大),也不可能是an(最小),
若2am=ak+an?2qm-k=1+qn-k,(*)
由2qm-k≤2q<1,1+qh-k>1,知(*)式不成立,
故ak,am,an不可能成等差数列.
(2)(ⅰ)(解法1)ak-ak+1-ak+2=a1qk-1(1-q-q2)=a1qk-1 ,
,
由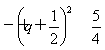 ∈
∈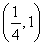 ,知ak-ak+1-ak+2<ak<ak-1<…,
,知ak-ak+1-ak+2<ak<ak-1<…,
且ak-ak+1-ak+2>ak+2>ak+3>…,
所以ak-ak+1-ak+2=ak+1,即q2+2q-1=0,
所以q=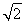 -1.
-1.
(解法2)设ak-ak+1-ak+2=am,则1-q-q2=qm-k,
由1-q-q2∈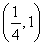 知m-k=1,即m=k+1,
知m-k=1,即m=k+1,
以下同解法1.
(ⅱ)bn=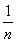 ,
,
(解法1)Sn=1+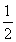 +
+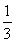 +…+
+…+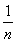 ,
,
Tn=1+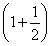 +
+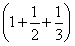 +…+
+…+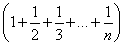
=n+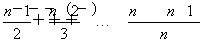 =n
=n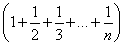 -
-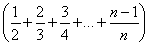
=nSn-[(1-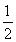 )+(1-
)+(1-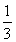 )+(1-
)+(1-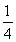 )+…+(1-
)+…+(1-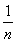 )]
)]
=nSn-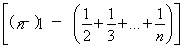 =nSn-
=nSn-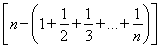
=nSn-n+Sn=(n+1)Sn-n,所以T2011=2012S2011-2011.
(解法2)Sn+1=1+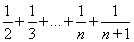 =Sn+
=Sn+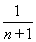 ,所以(n+1)Sn+1-(n+1)Sn=1,
,所以(n+1)Sn+1-(n+1)Sn=1,
所以(n+1)Sn+1-nSn=Sn+1,2S2-S1=S1+1,3S3-2S2=S2+1,……
(n+1)Sn+1-nSn=Sn+1,累加得(n+1)Sn+1-S1=Tn+n,
所以Tn=(n+1)Sn+1-1-n=(n+1)Sn-n=(n+1)(Sn+bn)-1-n
=(n+1)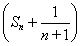 -1-n=(n+1)Sn-n,
-1-n=(n+1)Sn-n,
所以T2011=2012S2011-2011