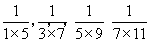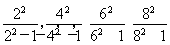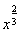题目内容
已知数列{an}的前n项和为Sn＝3n－1.
(1)求数列{an}的通项公式；
(2)若bn＝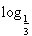
(Sn＋1)，求数列{bnan}的前n项和Tn.
（1）an＝2×3n－1（2）－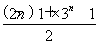
，n∈N*
【解析】(1)当n＝1时，a1＝S1＝2，
当n≥2时，an＝Sn－Sn－1＝(3n－1)－(3n－1－1)＝2×3n－1，综上所述，an＝2×3n－1.
(2)bn＝
(Sn＋1)＝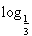
3n＝－n，所以bnan＝－2n×3n－1，
Tn＝－2×1－4×31－6×32－…－2n×3n－1，
3Tn＝－2×31－4×32－…－2(n－1)×3n－1－2n×3n，相减，得
－2Tn＝－2×1－2×31－2×32－…－2×3n－1＋2n×3n
＝－2×(1＋31＋32＋…＋3n－1)＋2n×3n，
所以Tn＝(1＋31＋32＋…＋3n－1)－n×3n＝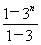
－n×3n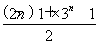＝－，n∈N*
练习册系列答案
相关题目
