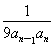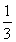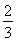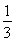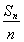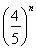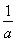题目内容
已知等比数列{an}中,a2=32,a8=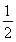 ,an+1<an.
,an+1<an.
(1)求数列{an}的通项公式;
(2)设Tn=log2a1+log2a2+…+log2an,求Tn的最大值及相应的n值.
(1)27-n(2)n=6或n=7时,Tn最大,其最大值是T6=T7=21
【解析】(1)q6= ,an+1<an,所以q=
,an+1<an,所以q=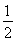 .以a1=
.以a1=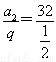 =64为首项,所以通项公式为an=64·
=64为首项,所以通项公式为an=64· n-1=27-n(n∈N?).
n-1=27-n(n∈N?).
(2)设bn=log2an,则bn=log227-n=7-n.所以{bn}是首项为6,公差为-1的等差数列.
Tn=6n+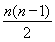 (-1)=-
(-1)=-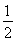 n2+
n2+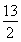 n=-
n=-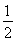 (n-
(n-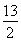 )2+
)2+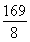 .因为n是自然数,所以n=6或n=7时,Tn最大,其最大值是T6=T7=21.
.因为n是自然数,所以n=6或n=7时,Tn最大,其最大值是T6=T7=21.

练习册系列答案
相关题目