题目内容
已知数列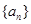 的前项和为
的前项和为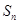 ,且满足
,且满足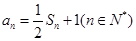 ;
;
(Ⅰ)求数列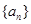 的通项公式;
的通项公式;
(Ⅱ)若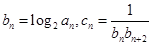 ,且
,且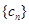 的前n项和为
的前n项和为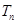 ,求使得
,求使得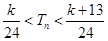 对
对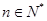 都成立的所有正整数k的值.
都成立的所有正整数k的值.
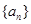 的前项和为
的前项和为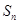 ,且满足
,且满足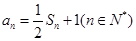 ;
;(Ⅰ)求数列
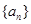 的通项公式;
的通项公式;(Ⅱ)若
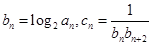 ,且
,且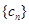 的前n项和为
的前n项和为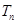 ,求使得
,求使得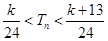 对
对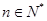 都成立的所有正整数k的值.
都成立的所有正整数k的值.(Ⅰ)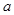 n=2n;(Ⅱ)5、6、7
n=2n;(Ⅱ)5、6、7
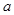 n=2n;(Ⅱ)5、6、7
n=2n;(Ⅱ)5、6、7试题分析:(Ⅰ)因为
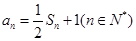 ,所以递推一个等式得到
,所以递推一个等式得到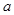 n-1=
n-1=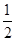 Sn-1+1(n≥2).再通过
Sn-1+1(n≥2).再通过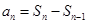 即可得到一个关于
即可得到一个关于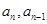 的等式,所以可得所求的结论.
的等式,所以可得所求的结论.(Ⅱ)由(Ⅰ)所得的结论,又因为
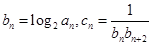 可以求出bn=n,,
可以求出bn=n,,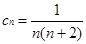 .所以数列
.所以数列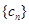 的前n项的和为
的前n项的和为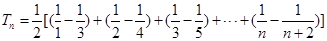 =
=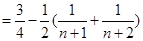 .又因为
.又因为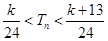 对
对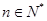 .所以必须满足
.所以必须满足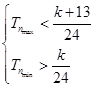 .即可求得k的范围,所以可求出结论.
.即可求得k的范围,所以可求出结论.试题解析:(Ⅰ)
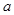 n=
n=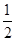 Sn+1 ①
Sn+1 ①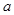 n-1=
n-1=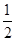 Sn-1+1(n≥2) ②
Sn-1+1(n≥2) ②①-②得:
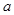 n=2
n=2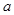 n-1(n≥2),又易得
n-1(n≥2),又易得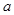 1=2 ∴
1=2 ∴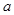 n=2n 4分
n=2n 4分(Ⅱ) bn=n,
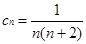
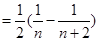
裂项相消可得
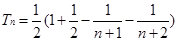
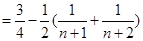 8分
8分∵
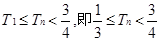 10分
10分∴欲
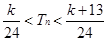 对n∈N*都成立,须
对n∈N*都成立,须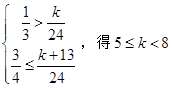 ,
,又k正整数,∴k=5、6、7 13分

练习册系列答案
相关题目
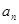
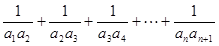
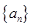 的前n项和为
的前n项和为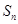 ,且
,且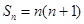 ,数列
,数列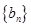 满足
满足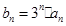 .
.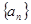 满足:
满足: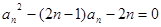 .
.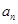 ;
;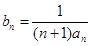 ,求数列
,求数列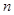 项和
项和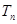 .
.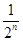 ,n∈N?,则a3=________.
,n∈N?,则a3=________.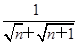 ,若{an}的前n项和为24,则n为________.
,若{an}的前n项和为24,则n为________.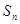 为等比数列
为等比数列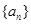 的前
的前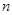 项和,若
项和,若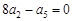 ,则
,则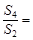 ( )
( )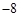



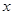 ,用
,用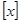 表示不超过
表示不超过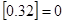 ,
,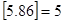 ,若
,若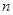 为正整数,
为正整数,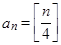 ,
,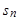 为数列
为数列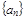 的前
的前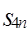 __________________________;
__________________________;