题目内容
1. 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.(1)求证:平面AA1C⊥平面BA1C.
(2)求几何体A1-ABC的体积V的最大值.
分析 (1)证明AC⊥BC,推出BC⊥平面AA1C,然后利用平面与平面垂直的判定定理证明即可.
(2)在Rt△ABC中,设AC=x,表示出BC,求出几何体的体积的表达式,利用二次函数的最值求解即可.
解答  (1)证明:∵C是底面圆周上异于A,B的一点,AB是底面圆的直径,
(1)证明:∵C是底面圆周上异于A,B的一点,AB是底面圆的直径,
∴AC⊥BC.(2分)
$\left.\begin{array}{l}A{A_1}⊥底面ABC\\ BC?平面ABC\end{array}\right\}⇒BC⊥A{A_1}$(3分)、
AA1∩AC=A,
$\left.\begin{array}{l}∴BC⊥平面A{A_1}C\\ BC?平面B{A_1}C\end{array}\right\}⇒平面A{A_1}C⊥平面B{A_1}C$(6分)
(2)解:在Rt△ABC中,设AC=x,
则$BC=\sqrt{A{B^2}-A{C^2}}=\sqrt{4-{x^2}}(0<x<2)$${V_{{A_1}-ABC}}=\frac{1}{3}{S_{△ABC}}•A{A_1}=\frac{1}{3}x\sqrt{4-{x^2}}=\frac{1}{3}\sqrt{{x^2}(4-{x^2})}=\frac{1}{3}\sqrt{-{{({x^2}-2)}^2}+4}$(10分)
当x2=2,即$x=\sqrt{2}$时,${V_{{A_1}-ABC}}$的最大值为$\frac{2}{3}$.(12分)
点评 本题考查平面与平面垂直的判定定理的应用,几何体的体积的求法,二次函数的性质,考查计算能力.

练习册系列答案
相关题目
12.函数$f(x)=\sqrt{1-{{log}_2}(x-1)}$的定义域为( )
| A. | (1,3] | B. | (-∞,3] | C. | (0,3] | D. | (1,3) |
9.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=$\frac{π}{3}$,记椭圆和双曲线的离心率分别为e1,e2,则$\frac{1}{{e}_{1}{e}_{2}}$的最大值为( )
| A. | 3 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{2\sqrt{3}}{3}$ |
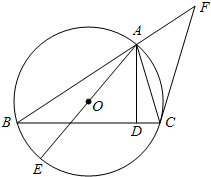 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.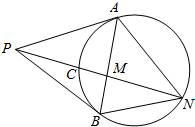
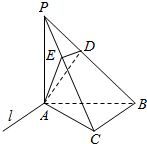 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.