题目内容
6.如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,求$\frac{BD}{DA}$.
分析 连CD,先在Rt△ABC中利用勾股定理求出AB=5cm,再分别利用Rt△ADC∽Rt△ACB和Rt△BDC∽Rt△BCA,求出AD和BD,然后得到它们的比.
解答 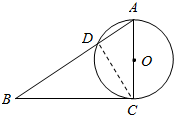 解:连CD,如图,
解:连CD,如图,
在Rt△ABC中,因为AC、BC的长分别为3cm、4cm,所以AB=5cm,
∵AC为直径,
∴∠ADC=90°,
∵∠A公共,
∴Rt△ADC∽Rt△ACB,
∴$\frac{AD}{AC}=\frac{AC}{AB}$,即$\frac{AD}{3}=\frac{3}{5}$,
∴AD=$\frac{9}{5}$,
同理可得Rt△BDC∽Rt△同理可得Rt△BDC∽Rt△BCA,
∴$\frac{BD}{BC}=\frac{BC}{AB}$,即$\frac{BD}{4}=\frac{4}{5}$,
∴BD=$\frac{16}{5}$,
∴$\frac{BD}{DA}$=$\frac{16}{9}$.
点评 本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆周角的推论:直径所对的圆周角为90度.也考查了勾股定理以及三角形相似的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
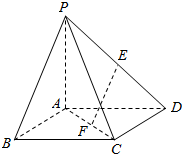 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).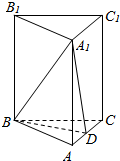 如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点.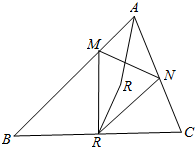 已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上.
已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上. 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2. 如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证:
如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证: