题目内容
10.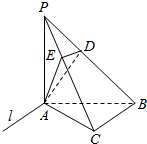 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.平面ADE∩平面ABC=l.(1)求证:DE∥l;
(2)求证:DE⊥平面PAC;
(3)若二面角A-DE-P为直二面角,求PE:PC的值.
分析 (1)假设DE与l不平行,由公理二得DE、l、BC交于同一点,这与已知DE∥BC相矛盾,由此能证明DE∥l.
(2)要证明DE⊥平面PAC,先证明BC⊥平面PAC,只需证明BC垂直平面PAC内的两条相交直线PA、AC即可.
(3)由已知得∠AEP=90°,∠PAC=90°,△PAC∽△PEA,设PA=AB=2,由已知条件能求出BC=1,AC=$\sqrt{3}$,PC=$\sqrt{7}$,PE=$\frac{P{A}^{2}}{PC}$,由此能求出PE:PC的值.
解答 (1)证明:∵平面ADE∩平面ABC=l,∴l与DE共面于平面ADE,
假设DE与l不平行,则DE与l相交,
∵DE∥BC,∴l与BC相交,
∴由公理二得DE、l、BC交于同一点,
这与已知DE∥BC相矛盾,故假设错误,
∴DE∥l.
(2)证明:∵PA⊥底面ABC,∴PA⊥BC,
又∠PCA=90°,∴AC⊥BC,∴BC⊥平面PAC,
∵DE∥BC,∴DE⊥平面PAC.
(3)∵DE⊥平面PAC,
又AE?平面PAC,PE?平面PAC,
∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角A-DE-P的平面角,
∵二面角A-DE-P为直二面角,∴∠AEP=90°,
∵PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,∴∠PAC=90°,
设PA=AB=2,则BC=1,AC=$\sqrt{3}$,PC=$\sqrt{4+3}$=$\sqrt{7}$,
∵∠APC=∠EPA,∠PAC=∠PEA,∴△PAC∽△PEA,
∴$\frac{PC}{PA}=\frac{PA}{PE}$,∴PE=$\frac{P{A}^{2}}{PC}$=$\frac{4}{\sqrt{7}}=\frac{4\sqrt{7}}{7}$,
∴PE:PC=$\frac{4\sqrt{7}}{7}$:$\sqrt{7}$=4:7.
点评 本题考查线线平面的证明,考查直线与平面垂直的判定,直线与平面所成的角,考查逻辑思维能力,空间想象能力,是中档题.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
| A. | ¬p:?x0∈(0,+∞),x02≥x0-1 | B. | ¬p:?x0∈(-∞,+0),x02≥x0-1 | ||
| C. | ¬p:?x0∈(0,+∞),x02<x0-1 | D. | ¬p:?x0∈(-∞,+0),x02<x0-1 |
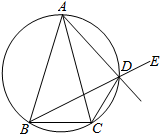 已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E.
已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E. 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.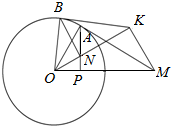 如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.
如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P. 如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD.
如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD.