题目内容
16.如图,PA,PB是圆O的两条切线,A,B为切点,PCN为圆O的割线,M为PN于AB的交点.证明:$\frac{AM}{BM}$=$\frac{A{N}^{2}}{B{N}^{2}}$.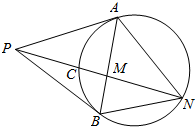
分析 证明△PAC∽△PNA,△PBC∽△PNB,可得BC:AC=BN:AN,利用△AMC∽△NMB,△BMC∽△NMA,即可证明结论.
解答 证明:∵PA,PB是圆O的两条切线,
∴△PAC∽△PNA,△PBC∽△PNB,
∴PA:PN=AC:AN,PB:PN=BC:BN,
∵PA=PB,
∴AC:AN=BC:BN,
∴BC:AC=BN:AN
又∵△AMC∽△NMB,△BMC∽△NMA,
∴BM:NM=BC:AN,MB:MC=NB:AC,
∴$\frac{B{M}^{2}}{NM•MC}$=$\frac{NB•BC}{AN•AC}$,
∴$\frac{B{M}^{2}}{BM•AM}$=$\frac{N{B}^{2}}{A{N}^{2}}$,
∴$\frac{AM}{BM}$=$\frac{A{N}^{2}}{B{N}^{2}}$.
点评 本题考查圆的切线的性质,考查三角形相似的判定与性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点为F1,F2.A,B为顶点,以线段F1F2为直径的圆交双曲线的一条渐近线bx-ay=0于M,N两点,且∠MAB=30°,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{21}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{5}{3}$ |
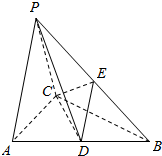 三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点.
三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点. 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.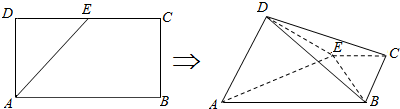
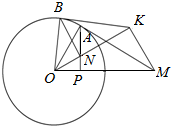 如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.
如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.