题目内容
9.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=$\frac{π}{3}$,记椭圆和双曲线的离心率分别为e1,e2,则$\frac{1}{{e}_{1}{e}_{2}}$的最大值为( )| A. | 3 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{2\sqrt{3}}{3}$ |
分析 先设椭圆的长半轴长为a1,双曲线的半实轴长a2,焦距2c.因为涉及椭圆及双曲线离心率的问题,所以需要找a1,a2,c之间的关系,而根据椭圆及双曲线的定义可以用a1,a2表示出|PF1|,|PF2|,在△F1PF2中根据余弦定理可得到:$\frac{1}{{{e}_{1}}^{2}}+\frac{3}{{{e}_{2}}^{2}}$=4,利用基本不等式可得结论.
解答 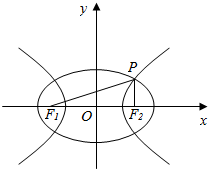 解:如图,设椭圆的长半轴长为a1,双曲线的半实轴长为a2,则根据椭圆及双曲线的定义:|PF1|+|PF2|=2a1,|PF1|-|PF2|=2a2,
解:如图,设椭圆的长半轴长为a1,双曲线的半实轴长为a2,则根据椭圆及双曲线的定义:|PF1|+|PF2|=2a1,|PF1|-|PF2|=2a2,
∴|PF1|=a1+a2,|PF2|=a1-a2,
设|F1F2|=2c,∠F1PF2=$\frac{π}{3}$,则:
在△PF1F2中由余弦定理得,
4c2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cos$\frac{π}{3}$
∴化简得:a12+3a22=4c2,
该式可变成:$\frac{1}{{{e}_{1}}^{2}}+\frac{3}{{{e}_{2}}^{2}}$=4,
∴$\frac{1}{{{e}_{1}}^{2}}+\frac{3}{{{e}_{2}}^{2}}$=4≥$\frac{2\sqrt{3}}{{e}_{1}{e}_{2}}$
∴$\frac{1}{{e}_{1}{e}_{2}}$≤$\frac{2\sqrt{3}}{3}$,
故选:D.
点评 本题考查圆锥曲线的共同特征,考查通过椭圆与双曲线的定义求焦点三角形三边长,解决本题的关键是根据所得出的条件灵活变形,求出焦点三角形的边长来.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.函数f(x)是奇函数,且在(0,+∞)内是单调递增函数,若f(3)=0,则不等式xf(x)<0的解集是( )
| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
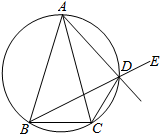 已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E.
已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E.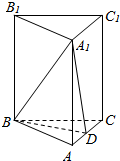 如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点.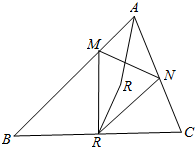 已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上.
已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上. 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.