题目内容
12.已知f(x)是定义在R上的不恒为零的函数,且对于任意实数a,b∈R满足f(a•b)=af(b)+bf(a),f(2)=2,an=$\frac{f({2}^{n})}{n}$(∈N+),bn=$\frac{f({2}^{n})}{{2}^{n}}$(n∈N+)考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;④数列{bn}为等差数列.
其中正确的结论是( )
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
分析 令x=y=0得f(0)=0,令x=y=1得f(1)=0判断①;用特例:f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2)判断②;利用题意得f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,求出an和bn,由等差、等比数列的定义判断③④.
解答 解:①、取a=b=0,可得f(0)=0,取a=b=1,可得f(1)=0,
∴f(0)=f(1),即①正确,
②、∵f(1)=f[(-1)•(-1)]=-2f(-1),
∴f(-1)=0,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),
故f(x)不是偶函数,②错;
又∵f(ab)=af(b)+bf(a),
∴f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n=…=n•2n,
∴an=2n,bn=n,
则数列{an}为等比数列,数列{bn}为等差数列,
∴①③④都正确,
故选:D.
点评 本题考查数列与抽象函数的综合运用,考查抽象函数的奇偶性,赋值法,等差数列,等比数列的定义及通项公式的特点,属于中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
17.已知a,b,c∈(0,1),并且a+b+c=2,则a2+b2+c2的取值范围是( )
| A. | ($\frac{4}{3}$,+∞) | B. | [$\frac{4}{3}$,2] | C. | [$\frac{4}{3}$,2) | D. | ($\frac{4}{3}$,2] |
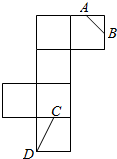 如图所示是一个正方体的表面展开图,A,B,C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为$\frac{\sqrt{10}}{5}$.
如图所示是一个正方体的表面展开图,A,B,C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为$\frac{\sqrt{10}}{5}$.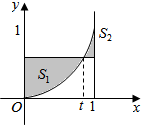 在区间[0,1]上给定曲线y=x2.
在区间[0,1]上给定曲线y=x2.