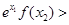题目内容
设f(x)=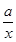 +xln x,g(x)=x3-x2-3.
+xln x,g(x)=x3-x2-3.
(1)如果存在x1,x2∈[0,2]使得g(x1)-g(x2)≥M成立,求满足上述条件的最大整数M;
(2)如果对于任意的s,t∈ ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.
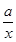 +xln x,g(x)=x3-x2-3.
+xln x,g(x)=x3-x2-3.(1)如果存在x1,x2∈[0,2]使得g(x1)-g(x2)≥M成立,求满足上述条件的最大整数M;
(2)如果对于任意的s,t∈
 ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.(1)4 (2) [1,+∞)
解:(1)存在x1,x2∈[0,2]使得g(x1)-g(x2)≥M成立,等价于[g(x1)-g(x2)]max≥M.
∵g(x)=x3-x2-3,
∴g′(x)=3x2-2x=3x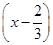 .
.
g(x),g′(x)随x变化的情况如下表:
由上表可知,g(x)min=g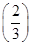 =-
=-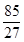 ,g(x)max=g(2)=1.
,g(x)max=g(2)=1.
[g(x1)-g(x2)]max=g(x)max-g(x)min=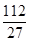 ,所以满足条件的最大整数M=4.
,所以满足条件的最大整数M=4.
(2)对于任意的s,t∈ ,都有f(s)≥g(t)成立,
,都有f(s)≥g(t)成立,
等价于在区间 上,函数f(x)min≥g(x)max.
上,函数f(x)min≥g(x)max.
由(1)可知,在区间 上,g(x)的最大值g(2)=1.
上,g(x)的最大值g(2)=1.
在区间 上,f(x)=
上,f(x)=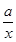 +xln x≥1恒成立.
+xln x≥1恒成立.
等价于a≥x-x2ln x恒成立,
记h(x)=x-x2ln x,
则h′(x)=1-2xln x-x,h′(1)=0.
当1<x<2时,h′(x)<0;当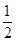 <x<1时,h′(x)>0,
<x<1时,h′(x)>0,
即函数h(x)=x-x2ln x在区间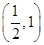 上单调递增,在区间(1,2)上单调递减,所以h(x)max=h(1)=1,即实数a的取值范围是[1,+∞).
上单调递增,在区间(1,2)上单调递减,所以h(x)max=h(1)=1,即实数a的取值范围是[1,+∞).
∵g(x)=x3-x2-3,
∴g′(x)=3x2-2x=3x
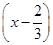 .
.g(x),g′(x)随x变化的情况如下表:
| x | 0 | 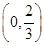 | 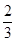 | 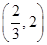 | 2 |
| g′(x) | 0 | - | 0 | + | |
| g(x) | -3 | ? | 极小值-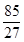 | ? | 1 |
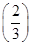 =-
=-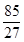 ,g(x)max=g(2)=1.
,g(x)max=g(2)=1.[g(x1)-g(x2)]max=g(x)max-g(x)min=
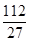 ,所以满足条件的最大整数M=4.
,所以满足条件的最大整数M=4.(2)对于任意的s,t∈
 ,都有f(s)≥g(t)成立,
,都有f(s)≥g(t)成立,等价于在区间
 上,函数f(x)min≥g(x)max.
上,函数f(x)min≥g(x)max.由(1)可知,在区间
 上,g(x)的最大值g(2)=1.
上,g(x)的最大值g(2)=1.在区间
 上,f(x)=
上,f(x)=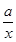 +xln x≥1恒成立.
+xln x≥1恒成立.等价于a≥x-x2ln x恒成立,
记h(x)=x-x2ln x,
则h′(x)=1-2xln x-x,h′(1)=0.
当1<x<2时,h′(x)<0;当
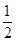 <x<1时,h′(x)>0,
<x<1时,h′(x)>0,即函数h(x)=x-x2ln x在区间
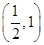 上单调递增,在区间(1,2)上单调递减,所以h(x)max=h(1)=1,即实数a的取值范围是[1,+∞).
上单调递增,在区间(1,2)上单调递减,所以h(x)max=h(1)=1,即实数a的取值范围是[1,+∞).
练习册系列答案
相关题目
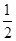 x2-
x2- 的取值范围.
的取值范围.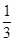 x3+
x3+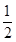 ax2+bx.
ax2+bx.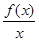 >0,若a=
>0,若a=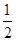 f
f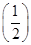 ,b=-2f(-2),c=ln
,b=-2f(-2),c=ln 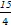 x-9都相切,则a等于( )
x-9都相切,则a等于( )
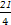
 或-
或-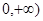 上的非负可导函数f(x)满足xf′(x)
上的非负可导函数f(x)满足xf′(x)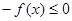 ,对任意正数
,对任意正数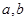 ,若满足
,若满足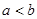 ,则必有( )
,则必有( )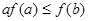
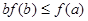
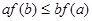
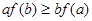
 x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.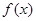 满足:
满足: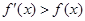 恒成立,若
恒成立,若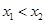 ,则
,则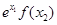 与
与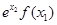 的大小关系为 ( )
的大小关系为 ( )