题目内容
已知函数f(x)=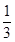 x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
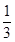 x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
由题意可知f′(x)=x2+2ax-b≤0在区间[-1,2]上恒成立,∴1-2a-b≤0且4+4a-b≤0,作出可行域如图,
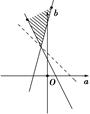
当直线经过两直线的交点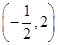 时,取得最小值
时,取得最小值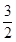 .
.

当直线经过两直线的交点
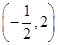 时,取得最小值
时,取得最小值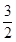 .
.
练习册系列答案
相关题目
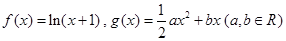 .
. 存在单调递减区间,求实数
存在单调递减区间,求实数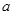 的取值范围;
的取值范围;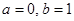 ,求证:当
,求证:当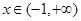 时,
时,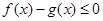 恒成立;
恒成立; ,证明:
,证明: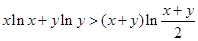 .
.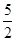 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;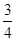 +
+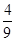 +…+
+…+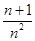 >ln(n+1)都成立.
>ln(n+1)都成立.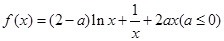 .
.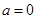 时,求
时,求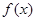 的极值;
的极值;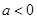 时,讨论
时,讨论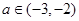 ,
,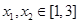 ,恒有
,恒有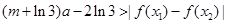 成立,求实数
成立,求实数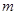 的取值范围.
的取值范围.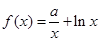 ,其中
,其中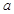 为实常数。
为实常数。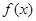 的单调性;
的单调性;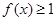 在
在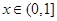 上恒成立,求实数
上恒成立,求实数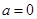 ,设
,设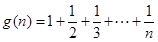 ,
,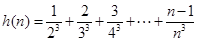
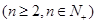 。是否存在实常数
。是否存在实常数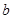 ,既使
,既使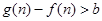 又使
又使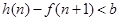 对一切
对一切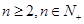 恒成立?若存在,试找出
恒成立?若存在,试找出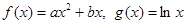 .
.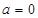 时,①若
时,①若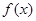 的图象与
的图象与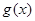 的图象相切于点
的图象相切于点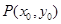 ,求
,求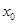 及
及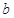 的值;
的值;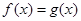 在
在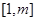 上有解,求
上有解,求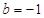 时,若
时,若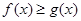 在
在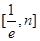 上恒成立,求
上恒成立,求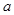 的取值范围.
的取值范围.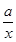 +xln x,g(x)=x3-x2-3.
+xln x,g(x)=x3-x2-3. ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.