题目内容
已知函数f(x)=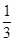 x3+
x3+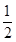 ax2+bx.
ax2+bx.
(1)若a=2b,试问函数f(x)能否在x=-1处取到极值?若有可能,求出实数a,b的值;否则说明理由.
(2)若函数f(x)在区间(-1,2),(2,3)内各有一个极值点,试求w=a-4b的取值范围.
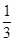 x3+
x3+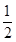 ax2+bx.
ax2+bx.(1)若a=2b,试问函数f(x)能否在x=-1处取到极值?若有可能,求出实数a,b的值;否则说明理由.
(2)若函数f(x)在区间(-1,2),(2,3)内各有一个极值点,试求w=a-4b的取值范围.
(1) 不能,理由见解析 (2) (-29,10)
解:(1)由题意f′(x)=x2+ax+b,
∵a=2b,∴f′(x)=x2+2bx+b.
若f(x)在x=-1处取极值,
则f′(-1)=1-2b+b=0,即b=1,
此时f′(x)=x2+2x+1=(x+1)2≥0,
函数f(x)为单调递增函数,这与该函数能在x=-1处取极值矛盾,
故该函数不能在x=-1处取得极值.
(2)∵函数f(x)=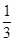 x3+
x3+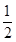 ax2+bx在区间(-1,2),(2,3)内分别有一个极值点,
ax2+bx在区间(-1,2),(2,3)内分别有一个极值点,
∴f′(x)=x2+ax+b=0在(-1,2),(2,3)内分别有一个实根,
∴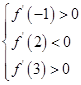 ⇒
⇒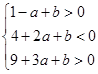
⇒
画出不等式表示的平面区域,如图所示,
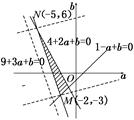
当目标函数w=a-4b过N(-5,6)时,
对应的w=-29;
当目标函数w=a-4b过M(-2,-3)时,
对应的w=10.
故w=a-4b的取值范围为(-29,10).
∵a=2b,∴f′(x)=x2+2bx+b.
若f(x)在x=-1处取极值,
则f′(-1)=1-2b+b=0,即b=1,
此时f′(x)=x2+2x+1=(x+1)2≥0,
函数f(x)为单调递增函数,这与该函数能在x=-1处取极值矛盾,
故该函数不能在x=-1处取得极值.
(2)∵函数f(x)=
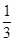 x3+
x3+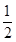 ax2+bx在区间(-1,2),(2,3)内分别有一个极值点,
ax2+bx在区间(-1,2),(2,3)内分别有一个极值点,∴f′(x)=x2+ax+b=0在(-1,2),(2,3)内分别有一个实根,
∴
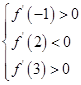 ⇒
⇒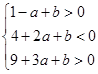
⇒

画出不等式表示的平面区域,如图所示,

当目标函数w=a-4b过N(-5,6)时,
对应的w=-29;
当目标函数w=a-4b过M(-2,-3)时,
对应的w=10.
故w=a-4b的取值范围为(-29,10).

练习册系列答案
相关题目
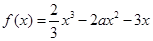 .
.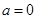 时,求曲线
时,求曲线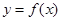 在点
在点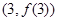 的切线方程;
的切线方程;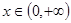 ,
,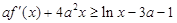 恒成立,求实数
恒成立,求实数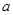 的取值范围;
的取值范围;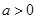 时,试讨论
时,试讨论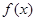 在
在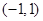 内的极值点的个数.
内的极值点的个数.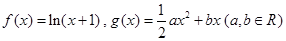 .
. 存在单调递减区间,求实数
存在单调递减区间,求实数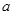 的取值范围;
的取值范围;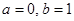 ,求证:当
,求证:当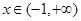 时,
时,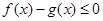 恒成立;
恒成立; ,证明:
,证明: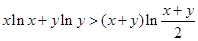 .
.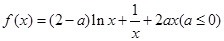 .
.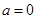 时,求
时,求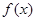 的极值;
的极值;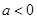 时,讨论
时,讨论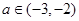 ,
,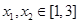 ,恒有
,恒有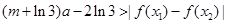 成立,求实数
成立,求实数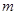 的取值范围.
的取值范围.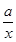 +xln x,g(x)=x3-x2-3.
+xln x,g(x)=x3-x2-3. ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.