题目内容
从某小组的2名女生和3名男生中任选2人去参加一项公益活动.
(1)求所选2人中恰有一名男生的概率;
(1)求所选2人中至少有一名女生的概率.
(1) ;(2)
;(2)
解析试题分析:先将2名女生和3名男生分别用字母表示,将随机抽取2人所包含的基本事件一一例举,(1)再将抽取的2人中恰有一男一女所包含的事件一一例举,根据古典概型概率公式可求其概率。(1)将抽取的2人中至少有一名女生所包含的事件一一例举,根据古典概型概率公式可求其概率。
试题解析:解析设2名女生为a1,a2,3名男生为b1,b2,b3,从中选出2人的基本事件有:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),(b1,b2),(b1,b3),(b2,b3),共10种.
(1)设“所选2人中恰有一名男生”的事件为A,则A包含的事件有:(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),共6种,
∴ ,
,
故所选2人中恰有一名男生的概率为 .
.
(2)设“所选2人中至少有一名女生”的事件为B,则B包含的事件有:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),共7种,
∴ ,
,
故所选2人中至少有一名女生的概率为 .
.
考点:古典概型概率。

练习册系列答案
相关题目

 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求 .
.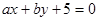 与圆
与圆 相切的概率;
相切的概率; 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率. ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数. 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 .
.