题目内容
(本小题满分12分)设数列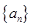 的前
的前 项和为
项和为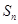 .已知
.已知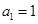 ,
, ,
, .
.
(Ⅰ)写出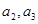 的值,并求数列
的值,并求数列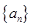 的通项公式;
的通项公式;
(Ⅱ)记 为数列
为数列 的前
的前 项和,求
项和,求 ;
;
(Ⅲ)若数列 满足
满足 ,
, ,求数列
,求数列 的通项公式。
的通项公式。
(Ⅰ) ,
, ,
, (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)
解析试题分析:(Ⅰ)由已知得, ,
, . ……………1分
. ……………1分
由题意, ,则当
,则当 时,
时, .
.
两式相减,得 (
( ). ……………2分
). ……………2分
又因为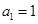 ,
, ,
, ,
,
所以数列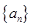 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以数列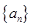 的通项公式是
的通项公式是 (
( ). ………4分
). ………4分
(Ⅱ)因为 ,
,
所以 , …5分
, …5分
两式相减得, , 整理得,
, 整理得, (
( ). …………………8分
). …………………8分
(Ⅲ) 当 时,依题意得
时,依题意得 ,
, ,… ,
,… ,  .
.
相加得, . …………10分
. …………10分
依题意 .
.
因为 ,所以
,所以 (
( ).
).
显然当 时,符合.
时,符合.
所以 (
( ). ……………12分
). ……………12分
考点:数列求和求通项
点评:本题主要涉及到的是由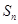 求通项,累和求通项,错位相减求和
求通项,累和求通项,错位相减求和

练习册系列答案
相关题目
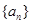 是公差
是公差 的等差数列,
的等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, .
. …),求数列
…),求数列 的前
的前 项和
项和 .
. 的通项公式为
的通项公式为 ,数列
,数列 的前n项和为
的前n项和为 ,且满足
,且满足
 中是否存在使得
中是否存在使得 是
是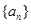 的前
的前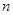 项和
项和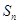 和通项
和通项 满足
满足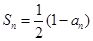 .
.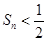 ;
;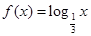 ,
,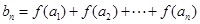 ,求
,求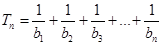 .
. 中,
中, ,
, (
( )
) ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:  .
.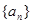 满足
满足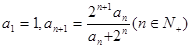
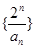 是等差数列; (2)求数列
是等差数列; (2)求数列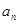 ;
; ,求数列
,求数列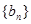 的前
的前 项和
项和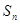 。
。 、
、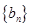 满足
满足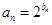
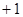 ,
,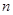 项和
项和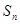 .
.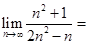 ___________.
___________.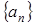 和等比数列
和等比数列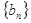 满足:
满足: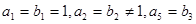 ,设
,设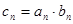 ,(其中
,(其中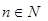 )。求数列
)。求数列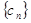 的通项公式以及前
的通项公式以及前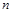 项和
项和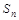 。
。