题目内容
(14分)已知数列 中,
中, ,
, (
( )
)
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:  .
.
(1)  ;(2)只需求出
;(2)只需求出 ,
,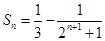 即可证明。
即可证明。
解析试题分析:(1)由 得
得 ,………………..3分
,………………..3分
又 ,所以
,所以 是等到比数列……………………………5
是等到比数列……………………………5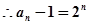 ,即
,即 ………………….………………7
………………….………………7
(2)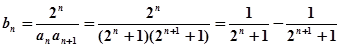 ………………………10
………………………10 ………….13
………….13 ……………………………. ….14
……………………………. ….14
考点:等比数列的性质;数列通项公式的求法;数列前n项和的求法。
点评:在求数列的通项公式时,常用的一种方法是构造新数列,通过构造的新数列是等差数列或等比数列来求。对于递推公式形如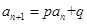 的形式,我们常用配凑系数构造新数列。
的形式,我们常用配凑系数构造新数列。

练习册系列答案
相关题目
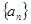 中,
中, 且点
且点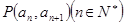 在直线
在直线 上。
上。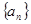 的通项公式;
的通项公式; (2)
(2)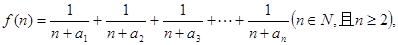 求函数
求函数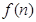 的最小值;
的最小值;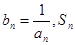 表示数列
表示数列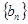 的前
的前 项和。试问:是否存在关于
项和。试问:是否存在关于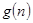 ,使得
,使得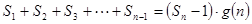 对于一切不小于2的自然数
对于一切不小于2的自然数 满足
满足 ,数列
,数列 满足
满足 ,
, 满足
满足 .
. ,证明数列
,证明数列 ,证明数列
,证明数列 的前
的前 项和
项和 满足
满足 。
。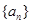 是公差为正的等差数列,其前
是公差为正的等差数列,其前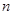 项和为
项和为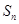 ,点
,点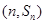 在抛物线
在抛物线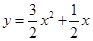 上;各项都为正数的等比数列
上;各项都为正数的等比数列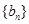 满足
满足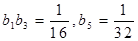 .
.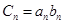 ,求数列
,求数列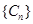 的前n项和
的前n项和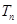 .
. 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
. 的值,并求数列
的值,并求数列 为数列
为数列 的前
的前 满足
满足 ,
, ,求数列
,求数列 的通项公式.
的通项公式.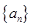 的前
的前 项和为
项和为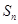 .已知
.已知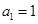 ,
, ,
, .
.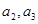 的值,并求数列
的值,并求数列 为数列
为数列 的前
的前 满足
满足 ,
, ,求数列
,求数列 的前n项和,求Tn.
的前n项和,求Tn. 的前
的前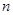 项和
项和 。(1)求数列
。(1)求数列 ,且数列
,且数列 的前
的前 。若
。若 ,求
,求