题目内容
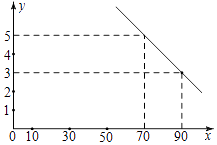
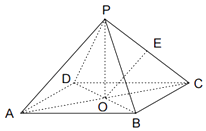
【题目】已知一四棱锥P﹣ABCD的三视图如图所示,E是侧棱PC上的动点. 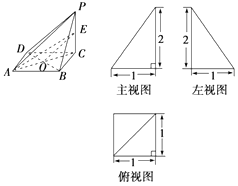
(Ⅰ)求四棱锥P﹣ABCD的体积.
(Ⅱ)若点E为PC的中点,AC∩BD=O,求证:EO∥平面PAD;
(Ⅲ)是否不论点E在何位置,都有BD⊥AE?证明你的结论.
【答案】(Ⅰ)解:由该四棱锥的三视图可知,该四棱锥P﹣ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2.
∴VP﹣ABCD= ![]() SABCDPC=
SABCDPC= ![]() .
.
(Ⅱ)证明:∵E、O分别为PC、BD中点
∴EO∥PA,
又EO平面PAD,PA平面PAD.
∴EO∥平面PAD.
(Ⅲ)不论点E在何位置,都有BD⊥AE,
证明如下:∵ABCD是正方形,
∴BD⊥AC,
∵PC⊥底面ABCD且BD平面ABCD,
∴BD⊥PC,
又∵AC∩PC=C,
∴BD⊥平面PAC,
∵不论点E在何位置,都有AE平面PAC,
∴不论点E在何位置,都有BD⊥AE.
【解析】(Ⅰ)四棱锥的底面是一个边长是1的正方形,一条侧棱与底面垂直,由这条侧棱长是2知四棱锥的高是2,求四棱锥的体积只要知道底面大小和高,就可以得到结果.(Ⅱ)利用三角形中位线的性质证明OE∥PA,由线面平行的判定定理可证EO∥平面PAD;(Ⅲ)不论点E在何位置,都有BD⊥AE,证明BD⊥平面PAC即可.

练习册系列答案
相关题目