题目内容
双曲线 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则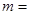 ( )
( )
 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则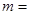 ( )
( )A.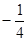 | B.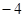 | C.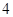 | D.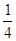 |
A
试题分析:由双曲线mx2+y2=1的虚轴长是实轴长的2倍,可求出该双曲线的方程,从而求出m的值.解:双曲线mx2+y2=1的虚轴长是实轴长的2倍,∴m<0,且双曲线方程为
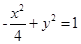 ,因此可知m的值为
,因此可知m的值为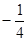 ,选A.
,选A.点评:本题考查双曲线性质的灵活运用,比较简单,需要注意的是m<0.

练习册系列答案
相关题目
题目内容
 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则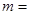 ( )
( )A.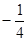 | B.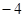 | C.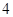 | D.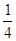 |
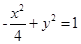 ,因此可知m的值为
,因此可知m的值为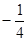 ,选A.
,选A.