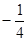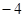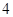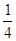题目内容
已知椭圆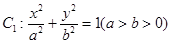 的右焦点
的右焦点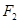 与抛物线
与抛物线 的焦点重合,左端点为
的焦点重合,左端点为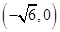
(1)求椭圆的方程;
(2)过椭圆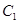 的右焦点且斜率为
的右焦点且斜率为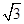 的直线
的直线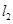 被椭圆
被椭圆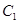 截的弦长
截的弦长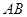 。
。
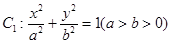 的右焦点
的右焦点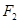 与抛物线
与抛物线 的焦点重合,左端点为
的焦点重合,左端点为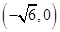
(1)求椭圆的方程;
(2)过椭圆
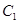 的右焦点且斜率为
的右焦点且斜率为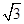 的直线
的直线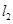 被椭圆
被椭圆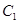 截的弦长
截的弦长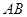 。
。(1)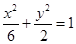 (2)
(2)
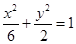 (2)
(2)
试题分析:解:(1)
 因为抛物线的焦点为
因为抛物线的焦点为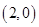 ,
,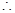
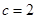 2分
2分又
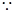 椭圆的左端点为
椭圆的左端点为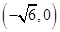
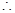
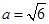 4分
4分则
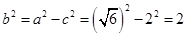 6分
6分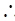 所求椭圆的方程为
所求椭圆的方程为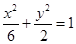 7分
7分⑵∴椭圆的右焦点
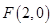 ,∴
,∴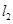 的方程为:
的方程为: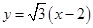 , 9分
, 9分代入椭圆C的方程,化简得,
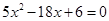 10分
10分由韦达定理知,
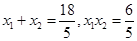 12分
12分从而
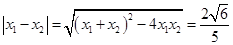
由弦长公式,得
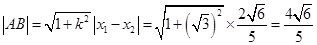 ,
,即弦AB的长度为
 14分
14分点评:解决的关键是利用联立方程组,结合韦达定理来求解,属于基础题。

练习册系列答案
相关题目
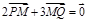 ,
,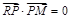 .
.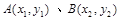 为轨迹C上两点,且
为轨迹C上两点,且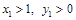 ,N(1,0),求实数
,N(1,0),求实数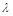 ,使
,使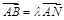 ,且
,且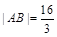 .
.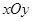 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为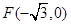 ,右顶点为
,右顶点为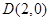 ,设点
,设点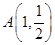 .
.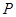 是椭圆上的动点,求线段
是椭圆上的动点,求线段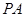 中点
中点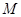 的轨迹方程;
的轨迹方程;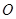 的直线交椭圆于点
的直线交椭圆于点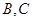 ,求
,求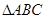 面积的最大值。
面积的最大值。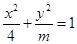 的焦距为2,则
的焦距为2,则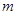 的值为( )
的值为( )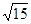
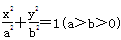 ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )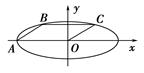
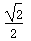
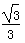
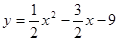 与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
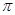 )。
)。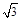 的直线与双曲线
的直线与双曲线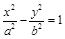 (a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
(a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是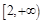
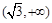
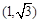
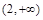
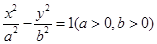 的右焦点F作与
的右焦点F作与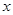 轴垂直的直线,分别与双曲线、双曲线的渐近线交于点
轴垂直的直线,分别与双曲线、双曲线的渐近线交于点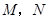 (均在第一象限内),若
(均在第一象限内),若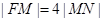 ,则双曲线的离心率为
,则双曲线的离心率为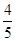
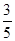
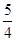
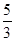
 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则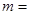 ( )
( )