Question

【题目】在平面四边形ABCD中，AB⊥BC，∠BCD＝120°，△ABD是边长为2的正三角形，E是AB边上的动点，则的最小值为_____．

Answer 1

【答案】

【解析】

将四边形放入坐标系，结合三角函数定义求出对应点的坐标，利用向量数量积公式转化为一元二次函数进行求求解即可．

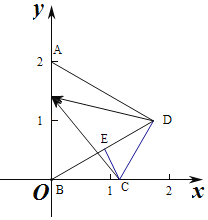
解：当四边形ABCD放入平面直角坐标系，

∵AB⊥BC，∠BCD＝120°，△ABD是边长为2的正三角形，

∴D（2cos30°，2sin30°），即D（，1），

∵∠CDB＝90°﹣60°＝30°，∠BCD＝120°

∴∠CDB＝30°，即△BCD是等腰三角形，

取BD的中点E，

则BE＝1，

则cos30°，

即BC，即C（，0），

设E（0，b），0≤b≤2，

则（，b﹣1），（，b），

则（，b﹣1）（，b）＝2+b（b﹣1）＝b2﹣b+2

＝（b）2+2═（b）2，

∴当b时，数量积取得最小值，

故答案为：